【刷题笔记】--dp--零钱兑换Ⅱ
创始人
2025-05-31 19:44:55

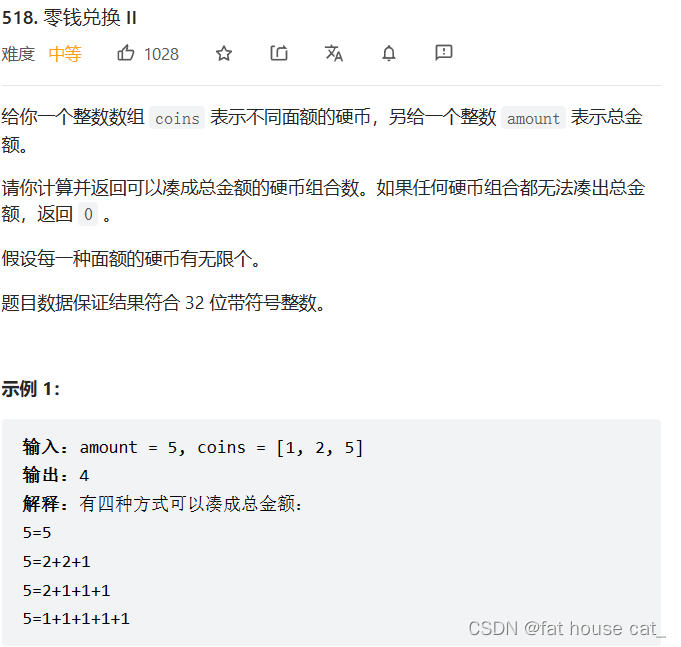
题目： 

 思路：

 拿示例1来看，我们的原问题是求dp[5]，表示金钱为5时，凑出该金额的硬币组合数，子问题自然就是dp[1]，dp[2]，dp[3]，dp[4]，现在的问题就是找到子问题与原问题的关系。

dp[5]是不是可以表示为当金额为4时的硬币组合后面都加上硬币1+当金额为3时的硬币组合后面都加上硬币2+当金额为0时的硬币组合后面都加上硬币1

即dp[5]=dp[4]+dp[3]+dp[0]（原理就是依次让5减去，coins数组里面的每一个数）

但是有个问题，就是会有重复组合的情况出现。

举个更简单的例子，

我们很容易知道dp[1]=1;（1）

                         dp[2]=2;（1+1或2）

如果按上面推理：dp[3]=dp[3-1]（2+1）（1+1+1）+dp[3-2]（1+2）=3;

 但很显然dp[3]=2 (1+1+1或1+2）

按上面的思路就是写两个for循环代码：

for(i=1;i

        for(j=0;j

                dp[i]+=dp[i-coins[j]];

        }

}

那要如何避免就是重复的问题呢？

看了别人的题解：发现他们的两个for循环和我的是对调的。即：

for(int i=0;i

 对于上面这个代码的理解，举个例子，对于dp[3]的计算，

dp[3]=dp[2] (1+1+1）       i=0的循环下

dp[3]=dp[1](1+2)              i=1的循环下

所以dp[3]=2;

所以就不会重复计算dp[3]=(2+1)

代码：

class Solution {public int change(int amount, int[] coins) {int[] dp=new int[amount+1];//定义一个dp数组dp[0]=1;for(int i=0;i

上一篇：从命令行向’git commit -m’添加换行符------转

下一篇：什么是队列，如何实现？

相关内容

热门资讯

铭记历史荣耀 积蓄统一大势 转自：贵州日报 历史回响激荡，时代步伐铿锵。岁末回望，2025年两岸关系在复杂严峻的风险挑战中...
贵阳综合保税区工业园区污染治理... 转自：贵州日报 （一）查阅途径 电话：18585743717；邮箱：1830656138...
获配金额超400亿元 浮盈比例... （来源：经济参考报） 2025年A股定增市场显著回暖，机构参与定增的热情也在攀升。Choice数据显...
补齐关键拼图 运营商首次入股个... （来源：经济参考报） 近日，朴道征信有限公司（以下简称“朴道征信”）正式引入中移投资控股有限责任公司...
《迎春图》与绵竹的春节传承 从画中走向画外：《迎春图》描绘的“打春”场景。清黄瑞鹄图据国家文物局官网　　四川绵竹年画最具代表性的...