03、栈和队列

1、栈的基本概念

逻辑结构:

操作受限的线性表：只允许在一端进行增加和删除的线性表。

特点：先进后出

卡特兰数：

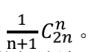
2、顺序栈的实现

定义：

typedef struct{int data[Maxsize];int top;
}Stack;

top是指向栈顶元素

进栈和出栈操作：

bool Push(SqStack *s,int x){if(s->top == -1){return false;}if(s->top >= Maxsize-1){return false;}s->top++;s->data[s->top] = x;return true;
} bool Pop(SqStack *s,int *x){if(s->top == -1){return false;}*x = s->data[s->top];s->top--;return true;
}

共享栈：

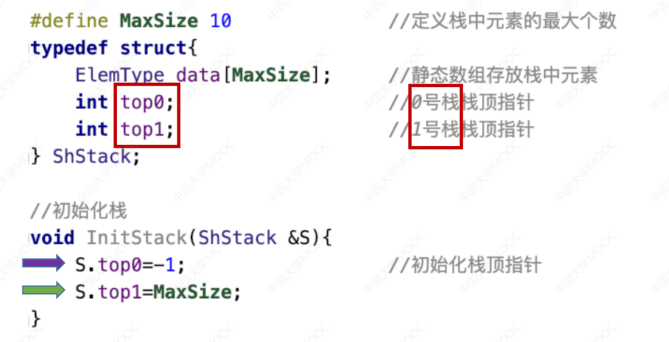
销毁时内存自动回收

3、链栈

和线性表当中的链表一样，只是进栈和出栈操作都是对头结点进行后插和后删操作一样。

//带头结点初始化
bool InitLink(LinkList *p){*p = (LNode*)malloc(sizeof(LNode));(*p)->next = NULL;return true; 
} 
//不带头结点初始化
bool InitnLink(LinkList *p){*p = NULL;return true; 
} 
//带头结点进栈 
bool PushLink(LinkList *p,int i){LNode * s = (LNode*)malloc(sizeof(LNode));s->data = i;s->next = (*p)->next;(*p)->next = s;return true;
}
//不带头结点进栈 
bool PushnLink(LinkList *p,int i){LNode * s = (LNode*)malloc(sizeof(LNode));s->data = i;s->next = *p;*p = s;return true;
}bool PopLinke(LinkList *p,int *i){LNode *s = (*p)->next;if(s == NULL){return false;}*i = s->data;(*p)->next = s->next;free(s);return true;
}
bool PopnLinke(LinkList *p,int *i){LNode *s = *p;if(s == NULL){return false;}*i = s->data;(*p) = s->next;free(s);return true;
}

4、队列

定义：操作受限的线性表

队尾输入，对头输出

先进先出的特点

1、顺序队列实现

//初始化队列操作，rear指向下一个可以存放的地址
bool InitSqQueue(SqQueue *s){s->front = 0;s->rear = 0;return true;
} 
//判断是否为空
bool EmptySqQueue(SqQueue s){if(s->front == s->rear){return true;}else{return false;}
} 
//入队
bool EnSqQueue(a *s,int i){if((s->rear + 1) % Maxsize == s->front){return false;}s->data[s->rear] = i;s->rear = (s->rear + 1) % Maxsize;return true;
} 
//出队
bool DeSqQueue(SqQueue *s,int *i){if(s->front == s->rear){return false;} i = s->data[s->front];s->front = (s->front + 1) % Maxsize;return true;
} 

2、队列链式实现

3、双端队列

5、括号匹配问题

思路：

如果是左括号，压入栈中。

如果是右括号，判断栈是否非空。

弹出栈顶元素，检查是否匹配。

最后结束的时候，判断栈是否非空。

bool bracketCheck(char str[],int length){int i;char x;LinkList L;InitLink(&L);for(i = 0;i < length;i++){if(str[i] == '(' || str[i] == '[' || str[i] == '{'){PushLink(&L,str[i]);}else{if(LinkeEmpty(L)){return false;}PopLinke(&L,&x);if(str[i] == ')' && x != '('){return false;}if(str[i] == ']' && x != '['){return false;}if(str[i] == '}' && x != '{'){return false;}}}return LinkeEmpty(L);
} 

6、表达式求值

中缀表达式为常规的表达式

后缀和前缀表达式是为了取消括号界限符，无歧义地表达运算规律

后缀&前缀表达式计算

后缀表达式手算的过程中

1、确定运算符生效顺序

2、确定运算符按照 ：左操作数 、右操作数、操作符的顺序组合成新的操作数

3、如果有剩余的数据继续2的操作

左优先：只要有同级别的运算符，先运算左边的

后缀表达式手算：

从左往右扫描，数字则入栈，遇到运算符则弹出2个元素，先出栈的为右操作数，运算之后再压入栈中。

前缀表达式：

遵循右优先原则，从右往左扫描，遇到数字压栈，先弹出栈顶的是左操作数，运算之后压入栈中。

中缀转后缀表达式

1. 定义一个栈用于存放操作符
2. 如果空栈，直接将操作符压栈
3. 如果再次遇到操作符
   1. 如果是左括号，直接压入栈
   2. 如果是右括号，一直出栈直到遇到左括号
   3. 如果是操作数，会弹出优先级等于或大于的运算符并且压入栈

计算中缀表达式

1、定义操作符栈（用于转换成后缀表达式）、操作数栈（用于计算后缀表达式）

1、扫描操作数，压入操作数栈。如果遇到操作符则压入栈，如果期间弹出栈，则弹出操作数栈并进行计算后重新压入栈。

7、递归函数栈

使用栈来存储递归函数的临时变量和语句，可能重复计算，增加空间复杂度

8、队列的应用

树的层序遍历、图的广度优先遍历

多线程先来先服务，就绪进程队列。