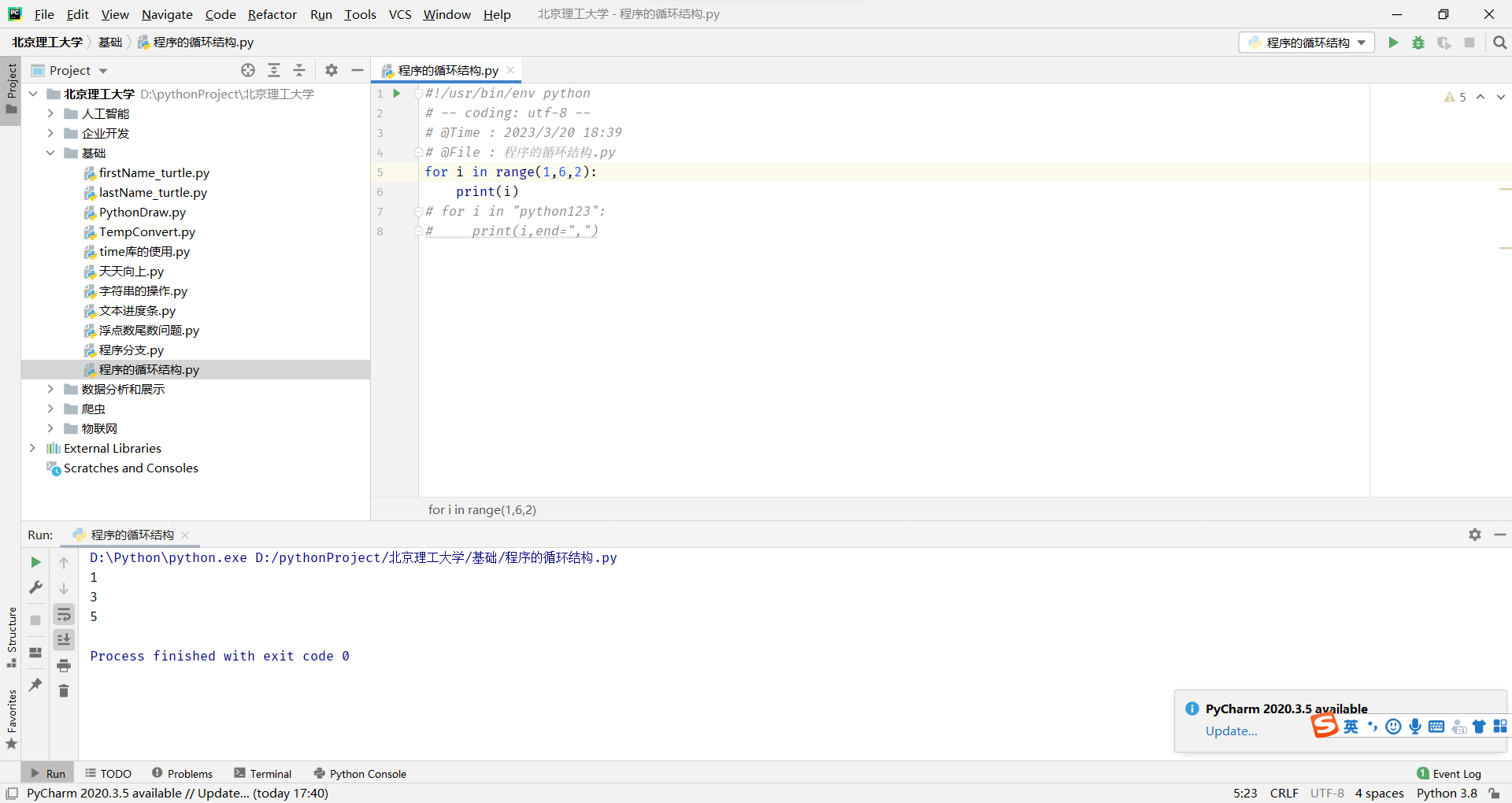
第三个参数就是步长 

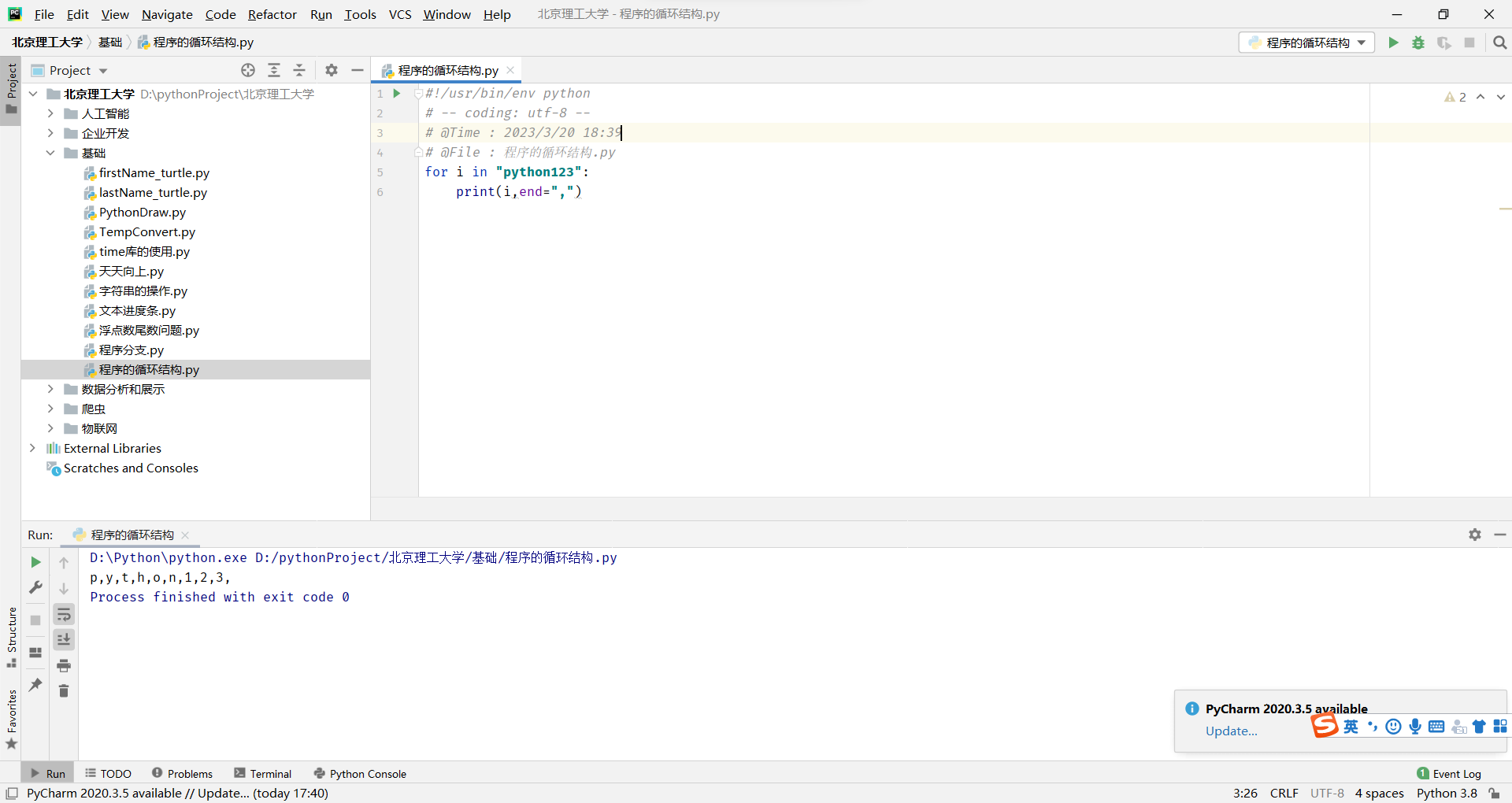
 引入文件时记得指明字符格式，否则读入不了

break结束循环，continue跳出本次循环 

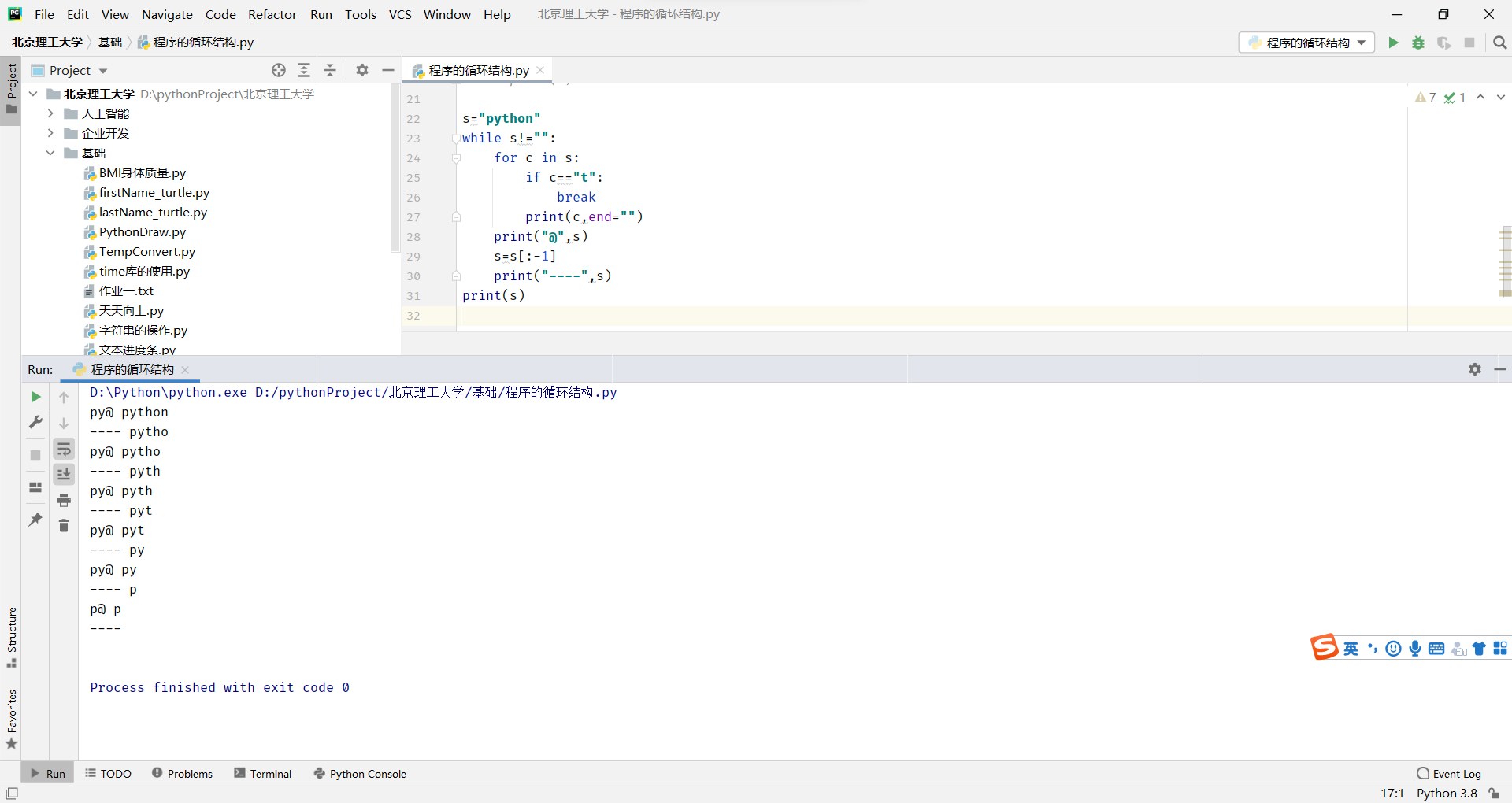
  一个break只能跳出一个循环

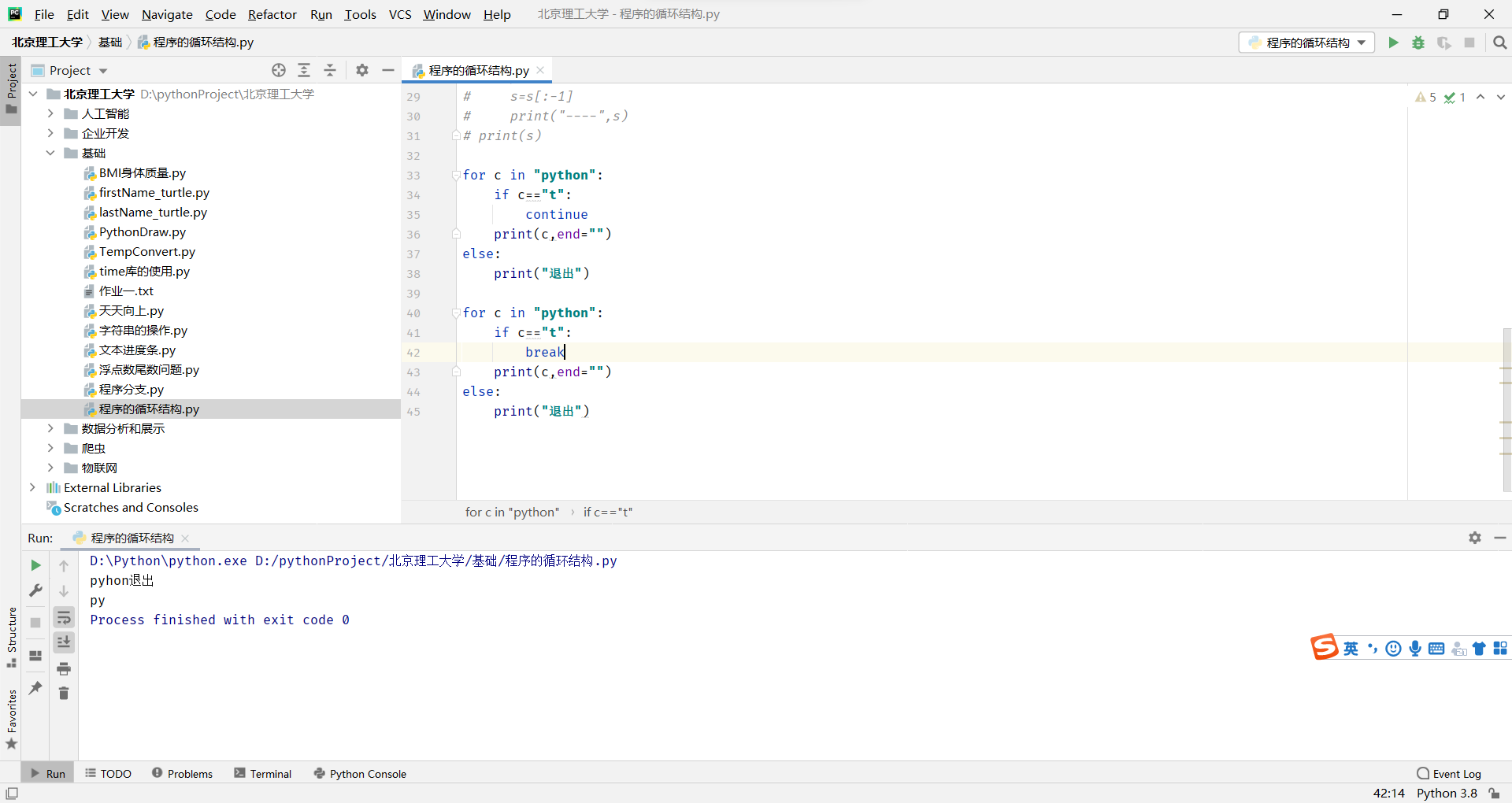
一定要注意是是break是退出当前循环，而不是条件判断 

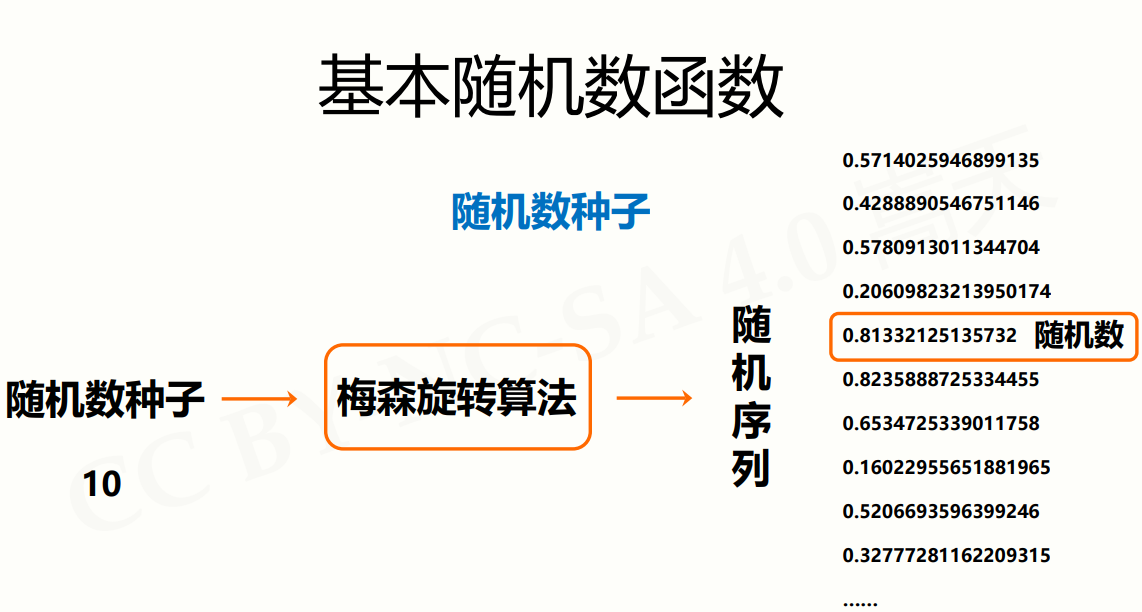
我们为什么要用随机数种子呢？

就是因为你编程中给出了随机数种子，那么下次程序再次运行，只要种子相同，那么产生的随机也相同，我们对于随机数的程序我们可以复现或者再现你程序运行的过程，如果不使用随机数种子，那么它默认使用的是当前系统时间，而那个时间是精确到微秒的，而这个时间是我们很难再现的，所以后面产生的程序运行的结果就是完全随机。

因此如果我们再现随机过程，我们就用随机种子

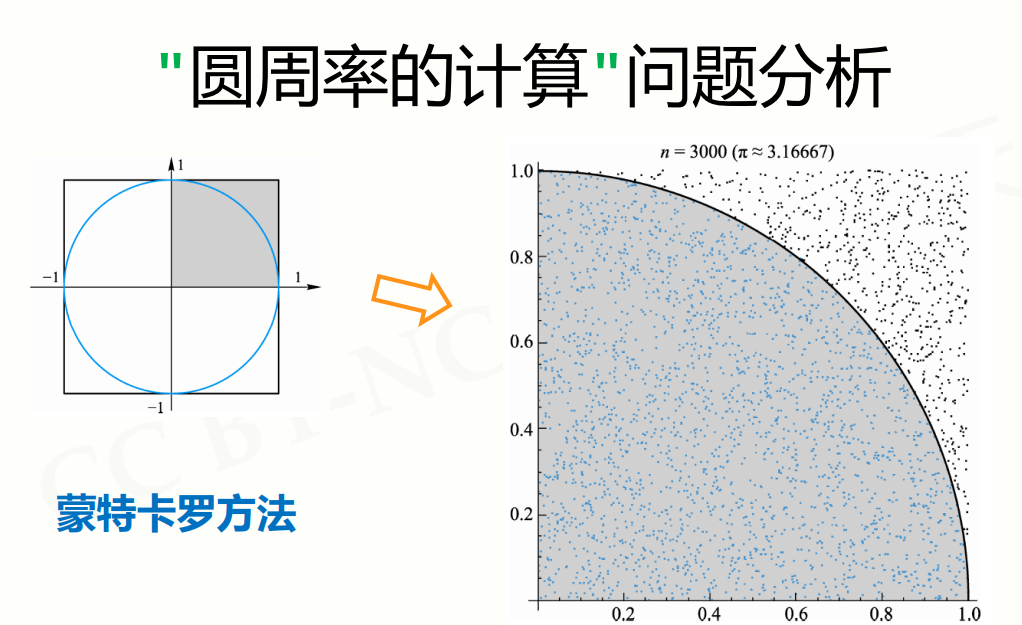
蒙特卡罗方法是一种通过随机取样来估计数学问题的方法。我们可以用蒙特卡罗方法来估计圆周率。

假设我们有一个边长为 2 的正方形，以及一个内切于该正方形的圆形。圆的半径为 1。

现在我们从正方形中随机取样若干个点，并计算它们与圆心的距离。如果距离小于等于 1，则该点在圆内，否则在圆外。

我们可以用这些采样点的比例来估计圆的面积与正方形面积之比。这个比例等于圆周率除以 4。

因为圆的面积为 πr²，而正方形面积为 4r²，所以它们的比例为 π/4。

因此，我们可以通过采样点的比例乘以 4 来估计圆周率。

具体的做法是，随机生成大量的点，计算在圆内的点的数量，然后用这个数量除以总的采样点数，再乘以 4，就可以得到圆周率的近似值。

需要注意的是，采样点数量越多，估计的圆周率就越精确。

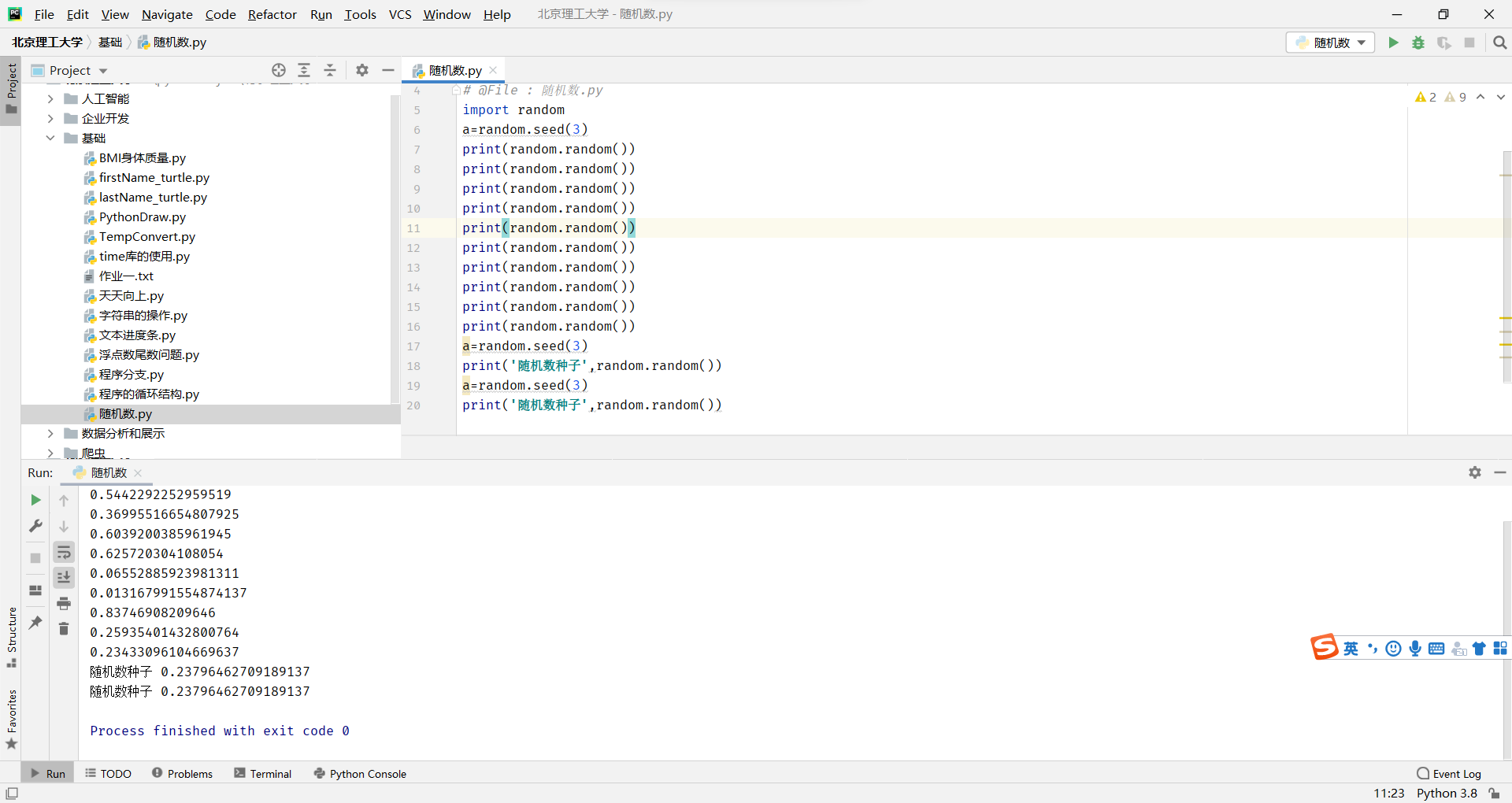
from random import random
from time import perf_counter
DARTS = 1000*1000
hits = 0.0
start = perf_counter()
for i in range(1, DARTS+1):x, y = random(), random()dist = pow(x ** 2 + y ** 2, 0.5)if dist <= 1.0:hits = hits + 1pi = 4 * (hits/DARTS)
print("圆周率值是: {}".format(pi))
print("运行时间是: {:.5f}s".format(perf_counter()-start))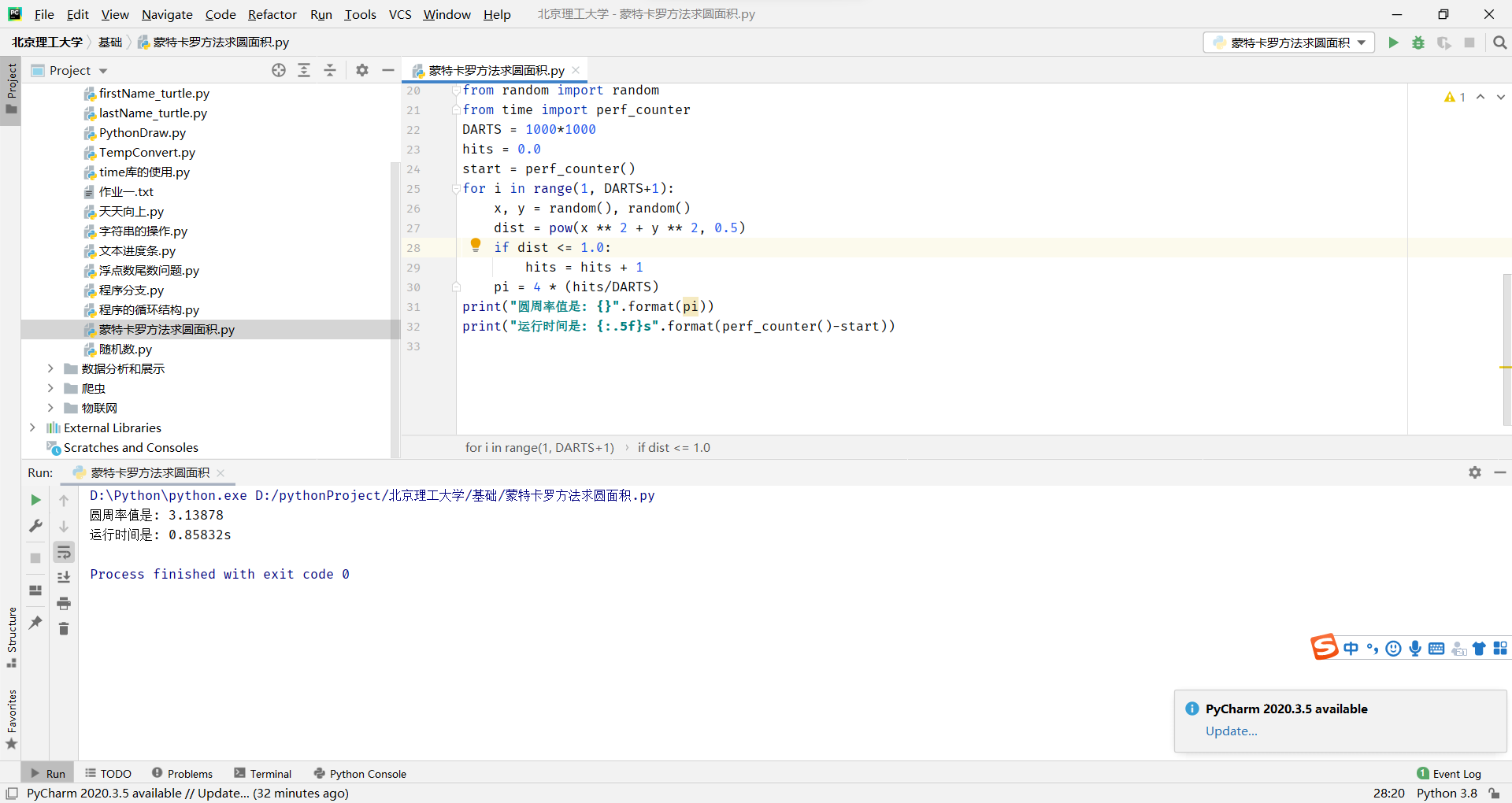

这段代码使用了蒙特卡罗方法来估计圆周率的值。下面是对代码的解剖：

导入 random 模块和 perf_counter 函数。

将常量 DARTS 设为 1000*1000，表示采样点数量。

定义变量 hits，初始值为 0.0，用于记录落在圆内的点的数量。

使用 perf_counter 函数记录开始时间。

使用 for 循环生成 DARTS 个采样点，每个点的横坐标和纵坐标都是一个 [0, 1) 之间的随机数。

计算采样点距离圆心的距离，如果距离小于等于 1，则将 hits 加 1。

根据蒙特卡罗方法，用 hits/DARTS 计算落在圆内的点的比例，再乘以 4，得到圆周率的近似值。

输出圆周率的近似值和运行时间。

需要注意的是，蒙特卡罗方法是一种概率方法，估计的圆周率并不是精确的值，而是一个近似值。因此，采样点数量越多，估计的值越接近真实值。在这段代码中，采样点数量为 1000*1000，可以得到较为准确的近似值。