多元线性回归

线性回归是机器学习中有监督机器学习下的一种算法。

回归问题主要关注确定一个唯一的因变量(dependent variable)(需要预测的值)和一个或多个数值型的自变量(independent variables)(预测变量)之间的关系。
需要预测的值：即目标变量，target，y，连续值
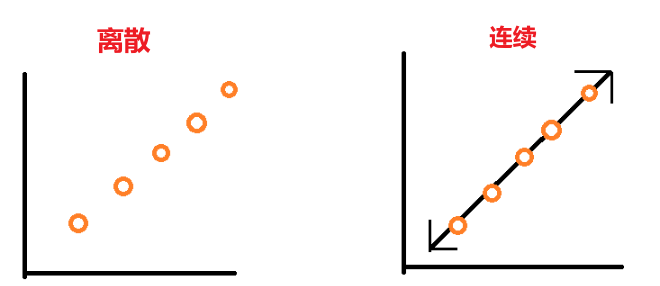
预测变量：影响目标变量的因素，predictors，X1…Xn，可以是连续值也可以是离散值
之间的关系：即模型，model，是我们要求解的

连续值和离散值

简单线性回归

前面提到过，算法说白了就是公式，简单线性回归属于一个算法，它所对应的公式。

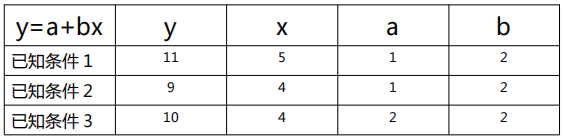
 y=a+bx

这个公式中，y 是目标变量即未来要预测的值，x 是影响 y 的因素，a,b 是公式上的参数即
要求的模型。其实 a 就是咱们的截距，b 就是斜率嘛！
所以很明显如果模型求出来了，未来影响 y 值的未知数就是一个 x 值，也可以说影响 y 值
的因素只有一个，所以这是算法包含“简单”这个词的原因。
同时可以发现从 x 到 y 的计算，x 只是一次方，所以这是算法叫“线性”回归的原因。

其实，大家上小学时就已经会解这种一元一次方程了。为什么那个时候不叫人工智能算法
呢？因为人工智能算法要求的是最优解！

最优解

Actual value：真实值，即已知的 y
Predicted value：预测值，是把已知的 x 带入到公式里面和猜出来的参数 a,b 计算得到的
Error：误差，预测值和真实值的差距
最优解：尽可能的找到一个模型使得整体的误差最小，整体的误差通常叫做损失 Loss
Loss：整体的误差，loss 通过损失函数 loss function 计算得到

多元线性回归

现实生活中，往往影响结果 y 的因素不止一个，这时 x 就从一个变成了 n 个，X1…Xn
同时简单线性回归的公式也就不在适用了

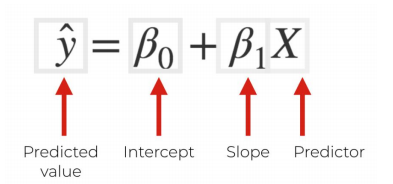
多元线性回归公式

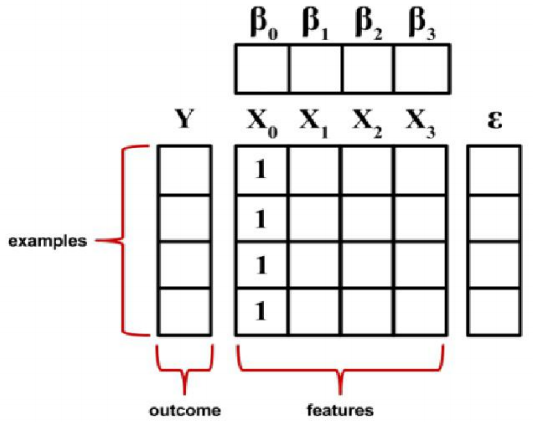
上图中，examples 就是已知的样本，examples 中包含 X 也包含 Y，Y 就是 outcome 已
知结果，如果咱们有 m 条历史记录，就是有 m 条样本，也就是有 m 个 Y 值，或者说 Y 为
包含 m 个值的一维向量。

同时每条样本的 X 从 X1 到 Xn 有 n 个影响结果的因素，图中为了简化相当于 n=3 即有 3
个影响结果的因素，在机器学习中，我们也会把影响结果的因素叫特征 feature，因为有多
个所以图里就是 features，值得一提的是 X0 一列，是为了后面可以通过公式计算出截距项
而加的，同时会把 X0 一列所有值设置恒为 1，这样 X 就是 m 行 4 列的二维数组即矩阵。
图中ε代表 error 误差，每条样本预测的值和真实值之间都会有误差，所以有 m 条样本就对
应 m 个ε值，ε和 Y 一样是包含 m 个值得一维向量。

最后图中还出现了β符号，从 0 到 n，n=3，总共有 4 个，其实细心的你会发现这个正好和
特征数量一样，我们可以理解或叫做这是特征的权值，代表对应特征的重要程度，也叫权重，
英文 weights，进而后面也会用符号 W 代替β。

深入理解线性回归

前面我们通过讲线性回归相信大家已经理解了回归任务是做什么的，但是还不知道具体怎么
做，就是说怎么求出最优解，为了透彻理解我们必须再补充一些概念，只有有了这些概念我
们后面才能推导出线性回归所需要的损失函数，进而去进一步理解最优解该如何去求。

理解回归一词来源

回归简单来说就是“回归平均值”(regression to the mean)。但是这里的 mean 并不是把
历史数据直接当成未来的预测值，而是会把期望值当作预测值。

中心极限定理

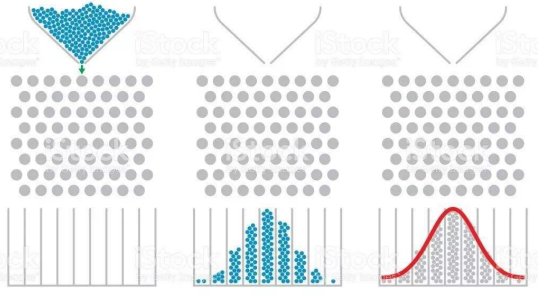
中心极限定理（central limit theorem）是概率论中讨论随机变量序列部分和分布渐近于正
态分布的一类定理。这组定理是数理统计学和误差分析的理论基础，指出了大量随机变量累
积分布函数逐点收敛到正态分布的积累分布函数的条件。

它是概率论中最重要的一类定理，有广泛的实际应用背景。在自然界与生产中，一些现象受到许多相互独立的随机因素的影响，如果每个因素所产生的影响都很微小时，总的影响可以看作是服从正态分布的。中心极限定理就是从数学上证明了这一现象 。

正太分布与预测的关系

也叫高斯分布

梯度下降法

归一化

正则化

Lasso回归_Ridge回归_多项式回归