遍历二叉树线索二叉树
遍历二叉树
遍历定义
- 顺着某一条搜索路径寻访二叉树中的每一个结点,使得每个节点均被依次访问,而且仅被访问依次(又称周游)
- “访问”的含义很广,可以是对结点作各种处理,如:输出结点的信息、修改节点的数据值等,但要求这种访问不被破坏原来的数据结构
遍历目的
- 得到树中所有结点的一个线性排列
遍历用途
- 它是树结构插入、删除、修改、查找和排序运算的前提,是二叉树一切运算的基础和核心。
遍历方法
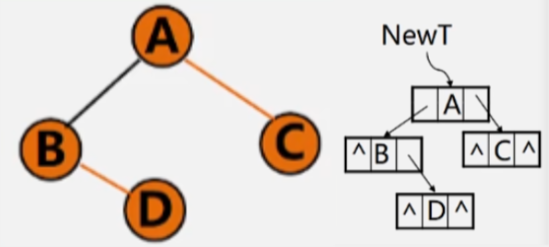
- 回顾二叉树的递归定义可知,二叉树是由 3 个基本单位构成的:根节点、左子树和右子树。若能依次遍历这三部分,就是遍历了整个二叉树。
- 假设:L:遍历左子树,D:访问根结点,R:遍历右子树。则可以有 DLR、LDR、LRD、DRL、RDL、RLD 这 6 种遍历二叉树的方案。
- 若规定先左后右,则只有前三种情况:
- DLR——先(根)序遍历。
- LDR——中(根)序遍历。
- LRD——后(根)序遍历。
- 第一个访问根结点就称为先序遍历,第二个访问根节点称为中序遍历,后序遍历同理。

算法描述
由二叉树的递归定义可知,遍历左子树和遍历右子树可如同遍历二叉树一样 递归 进行

先序遍历
若二叉树为空,则空操作;否则执行以下操作:
- 访问根结点
- 先序遍历左子树
- 先序遍历右子树
牢记按照 根左右 的顺序来进行遍历。每个结点的左子树的所有结点遍历完了之后才能轮到右子树。当一个结点的左右子树都为空的时候表示访问完毕。

算法实现
- 先访问这棵树的根节点 T 。
- 然后用同样的方法去递归访问左子树,将左子树的根结点T ->lchild 传给函数PreOrderTraverse。
- 当子树的某个结点为空的时候,返回上一层。
- 当左子树遍历完毕的时候,然后再继续递归遍历右子树。
//前趋(先序)遍历
void Pre(BiTree* T)
{//二叉树及二叉树底下的所有子树中,//某一棵树不为空时,执行以下操作if(T != NULL){printf("%d\n",T -> data);//输出根节点的值pre(T -> lchile);//以同样的先序遍历的方法遍历左子树pre(T -> rchile);//以同样的先序遍历的方法遍历右子树//当左、右子树的某个结点为空时,//返回该结点的递归的上一层}
}
- 反复的执行根左右的顺序,遍历每个小树。
- 当有不为空的树时,就得执行根左右
- 这样一层一层的深入,当执行完毕的时候再一层一层的返回。
- 直到第一次调用的根左右执行完毕的时候,才返回到主函数。
中序遍历
- 按照 左根右 的顺序进行遍历,根节点之下的每一棵二叉树都按照左根右的顺序遍历。
- 左子树按照 左根右 的顺序访问完所有结点之后才能访问根结点,最后右子树同样按照 左根右 的顺序访问所有结点。
若二叉树为空,则空操作;否则执行以下操作:
- 中序遍历左子树。
- 访问根结点。
- 中序遍历右子树。
每个结点的左子树按照左根右的顺序访问完了之后,才能访问根结点,最后按照 左根右 的顺序访问该结点的右子树的所有结点。

后序遍历
每个结点都按照左右根的顺序访问结点,每个结点的左子树按照左右根的顺序访问完所有结点之后,再到该结点的右子树按照左右根的顺序访问所有结点,最后访问该结点。
若二叉树为空,则空操作;否则执行以下操作:
- 后序遍历左子树。
- 后序遍历右子树。
- 访问根结点。

应用
根据遍历序列确定二叉树
- 若二叉树中各结点的值均不相同,则二叉树结点的先序序列、中序序列和后序序列都是唯一的。
- 由二叉树的先序序列和中序序列,或者由二叉树的后序序列和中序序列可以确定唯一一棵二叉树。
- 由先序序列和后序序列不能确定一棵树的原因是,不能确定哪个结点是根。
已知先序和中序序列求二叉树
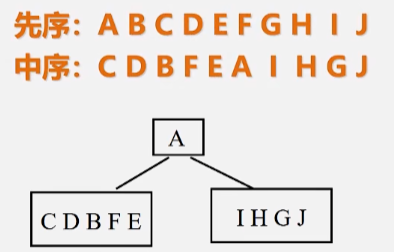
已知二叉树的先序和中序序列,构造出相应的二叉树。
- 先序(根左右):A B C D E F G H I J
- 中序(左根右):C D B F E A I H G J
- 对于一棵大树来说,先序遍历的第一个结点 A 肯定就是根节点。
- 在中序遍历中找到根结点 A 了之后,就能确定,根节点 A 左边的结点 CDBFE,一定在左子树上,右子树同理为 IHGJ。
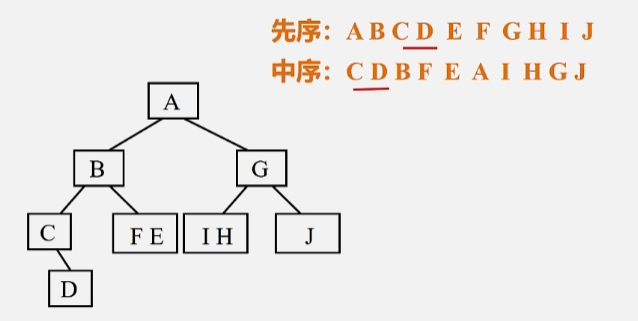
- 左子树按照先序排列的话第一个结点 B 一定是根。
- 同理,知道 B 是根的话,按照中序 B 左边的结点一定在 B 的左子树位置,FE 则在 B 的右子树位置。

- 同理,按照先序排列 A 的右子树的第一个结点就是G,G 左边的结点 HI 为左子树,J 为 G 的右子树

- 按照先序来看,对于 CD 来说,C 在前面,所以 C 是根,又按照中序看,D 在根 C 的后面(右边),所以 D 为 C 的右子树。
- 同理,由 FE 构成的树
- 按先序看,E 在前,所以 E 为根。
- 按中序看,F 在根 E 的前面,所以 F 在 E 的左子树。

- 在 HI 这棵子树上,
- 由先序看:H 在前,所以 H 为根。
- 有中序看:I 在前,所以 I 为 H 的左子树
最后就剩个 J 结点,所以不用再往后分了。

至此,这棵二叉树构造完成。
已知中序序列和后序序列求二叉树
已知一棵二叉树的中序和后序序列,请画出这棵二叉树。
- 中序(左根右)序列:B D C E A F H G
- 后序(左右根)序列:D E C B H G F A
- 由后序遍历可知,最后一个结点 A 一定是整棵树的根节点。
- 中序当中,知道 A 是根的话,那么 A 左边的结点 BDCE 就是左子树,右子树就是 FHG。
- 由中序(左根右)可知,第一个结点 B 一定是左子树的根,由后序(左右根)可知,找到结点B,B 结点左边的结点 DEC,就是以 B 为根的这棵树底下的所有结点。
- 由中序判断 DCE 都在 B 的右子树上,在后序中又能判断出 C 是 B 的右子树的根,由中序判断根 C 的左、右子树分别是 D、E。

- 由后序知,右子树的根是F,由中序知,HG 在根 F 的后边(左根右,在根的后边的肯定都在右子树上),此时就剩个 HG了,由后序可知,G 在 H 的后面,说明 G 为根,且由中序判断,H 在 G 的左边,说明 H 是 G 的左子树。

遍历二叉树的代码实现
/*二叉树的顺序存储*/
#include
#include#define MaxSize 100int data[MaxSize]; //数组存储树的结点,初始化为-1void init() //初始化数组
{for (int i = 0; i < MaxSize; i++){data[i]=-1;}
}//插入结点
void insert(int val)
{int i=1; //从根节点开始查找while (data[i]!=-1){ // 查找到空位置if(val - 以上三种算法非常相似,只有输出根结点的位置不一样。
- 在先序遍历中将访问根结点的位置放在第一位,中序就放在中间,后序最后。
- 如果将以上三种算法中访问根节点的这段语句拿走,这三个算法是完全相同的。
- 或者说三中算法的访问路径是相同的,只是访问结点的时机不同而已。

从上图看:
- 从虚线出发到终点的路径上,每个结点经过三次。
- 第一次经过时访问 = 先序遍历。
- 第二次经过时访问 = 中序遍历。
- 第三次经过时访问 = 后序遍历
- 第一次路过某个根结点的时候直接访问它,就相当于是先序遍历,如果将该结点的左子树访问完了之后,再回来访问该结点就是中序,后序同理。
时间复杂度
- 这三中算法的时间复杂度都是相同的,有 n 个结点的话就要遍历 n 个结点。
- 所以这三种算法的时间复杂度都为 O(n)。
空间复杂度
- 当遇到某个结点的时候,如果不访问它,就得找个空间将它记下来(这个结点没被访问),等回来的时候再来访问。
- 在最坏的情况下(单支二叉树),每个路过的结点都不访问都要存起来。
- 所以这三中算法最坏请况下的空间复杂度为 O(n)。
遍历二叉树的非递归算法
中序遍历非递归算法
- 二叉树中序遍历的非递归算法的关键:在中序遍历过某个结点的整个左子树后,如何找到该结点的根以及右子树。
基本思想:
- 建立一个栈
- 根节点进栈,遍历左子树
- 根节点出栈,输出根节点,遍历右子树
例:
下图所示的一颗二叉树的非递归遍历

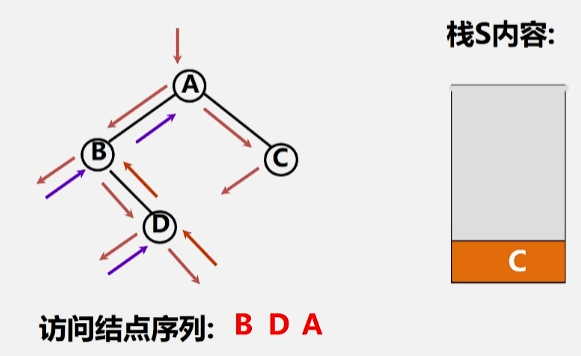
- 首先,遇到根节点 A 的时候不能访问它,必须先存到栈里头。

- 然后去访问 A 的左子树,同样的,B 结点为它所在的这棵树的根,先不能访问,得存进栈里。
- 将 B 存进栈里头了之后,再去访问 B 的左子树,发现左子树为空,这时候就该访问 B 结点了,所以将根结点 B 出栈。


- 接下来就去访问 B 这个根结点的右子树 D 了。
- 到了右子树之后还是先遇到了根结点 D(存起来)。

- 然后继续访问 D 的左子树,左子树为空,将 D 出栈,继续访问当前出栈元素(D)的右子树,右子树为空,此时 A 的左子树遍历完毕,将 A 出栈。

- 根结点访问完毕(出栈)之后,就该去访问该结点的右子树了。
- 同样,遇到根(C)的时候不能访问,得先存起来,直到它的左子树为空的时候,就可以回头来访问(出栈)该结点了。
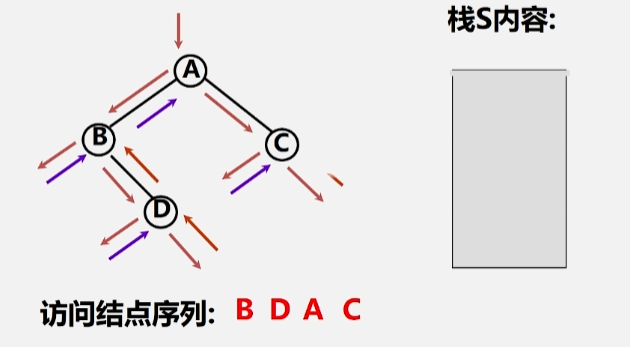
- 最后再访问刚出栈元素(C)的右子树,右子树为空的时候,回去看看栈里头还有没有元素,栈空的话则说明整趟遍历完成。
完整代码
#include
#include//定义二叉树结点结构体
typedef struct TreeNode{int data;struct TreeNode* left;struct TreeNode* right;}TreeNode;//定义栈结构体
typedef struct Stack{int top; //栈顶指针int capacity; //栈容量TreeNode **array; //栈数组,存放二叉树结点指针
}Stack;//创建二叉树结点
TreeNode* createNode(int data)
{TreeNode *node=(TreeNode*)malloc(sizeof(TreeNode)); //动态分配内存空间node->data=data; //赋值结点数据node->left=NULL; //初始化左右子结点为空node->right=NULL;return node; //返回新创建的结点
}//创建栈
Stack * createStack(int capacity)
{Stack *stack=(Stack*)malloc(sizeof(Stack)); //创建栈结构体stack->top=-1; //初始化栈顶指针stack->capacity=capacity; //设置栈容量stack->array=(TreeNode**)malloc(capacity * sizeof(TreeNode*)); //创建栈数组,存放二叉树结点指针return stack; //返回栈结构体指针
}//判断栈是否为空
int isEmpty(Stack* stack)
{return stack->top == -1; //当栈顶指针为-1时,说明栈为空
}//判断栈是否已满
int isFull(Stack* stack)
{return stack->top == stack->capacity -1 ; //当栈顶指针等于栈容量减1时,说明栈已满
}//入栈
void push(Stack* stack, TreeNode* node)
{if(isFull(stack)) //如果栈已满,则无法入栈{return ;}++stack->top;//栈顶指针先加1;然后将结点指针存放到栈顶stack->array[stack->top] = node;
}//出栈
TreeNode* pop(Stack* stack)
{if(isFull(stack)) //如果栈为空,则无法出栈{return NULL;}return stack->array[stack->top--]; //先取出栈顶结点指针,然后栈顶指针-1
}//中序遍历二叉树的非递归方法
void inorderTraversal(TreeNode* root)
{if(root == NULL) //如果根节点为空,则直接返回{return ;}Stack * stack= createStack(100); //创建一个栈,容量为100TreeNode * current =root; //初始化当前结点为根结点while(current != NULL || !isEmpty(stack)) //当当前结点不为空,或者栈不为空时,循环执行以下代码{//先将当前结点及其左子树全部入展while (current != NULL) //当前结点不为空时,将当前结点及其左子树全部入栈{push(stack,current); //将当前结点入栈current = current->left; //当前结点指向其左子节点}//已经遍历完了当前结点的所有左子节点,现在从栈中取出第一个结点current = pop(stack); //取出栈顶结点printf("%d",current->data); //输出该结点的值current = current->right; //将当前结点指向其右子结点,继续遍历右子树}
}int main(){//创建二叉树// 创建二叉树TreeNode* root = createNode(1);root->left = createNode(2);root->right = createNode(3);root->left->left = createNode(4);root->left->right = createNode(5);root->right->left = createNode(6);root->right->right = createNode(7);// 中序遍历二叉树inorderTraversal(root);return 0;
}
层序遍历二叉树
- 层次遍历:顾名思义就是按照二叉树的层数来遍历,第一层遍历完了之后遍历第二层,接着第三次以此类推。
- 对于一棵二叉树,从根结点开始,按照从上到下、从左到右的顺序访问每一个结点,且每个结点只访问一次。
- 层次遍历结果:a b f c d g e h

算法思路:使用一个队列
- 将根结点进队;
- 队不为空时执行循环:不断从队伍中出队一个结点 *p,访问这个结点:
- 若它有左孩子结点,将左孩子结点进队;
- 若它有右孩子结点,将右孩子结点进队。
例如:
- 先将根节点a 入队

- 然后将当前队列当中的根结点 a 出队,在出队的同时,判断该结点时候有左右孩子,若有,则存进队中。

- 若队列当中还有元素,则继续出队,将 b 出队执行上述步骤,将 b 结点的左右孩子入队。

- 将 f 结点出队,将 f 的左孩子 g 入队。

- 将 c 出队,c 无左右孩子,所以不管。d 出队,e 入队。g出队,h入队,然后依次出队,直到队空位置。




#include "stdlib.h"
#include "stdio.h"//定义二叉树结点结构体
struct TreeNode{int val; //结点的值struct TreeNode* left; //左子节点执照怎struct TreeNode* right; //右子结点指针
}TreeNode;//定义队列结构体
struct Queue{struct TreeNode* data; //存储结点指针的数组int front; //队头指针int rear; //队尾指针
} Queue;//初始化队列
void initQueue(struct Queue *q,int MaxSize )
{q->data=(struct TreeNode*)malloc(MaxSize * sizeof(struct TreeNode)); //申请数组空间q->front=0; //队头指针初始化为0q->rear=0; //队尾指针初始化为0
}//判断队列是否为空
int isEmpty(struct Queue* q)
{return q->front == q->rear; //当队头指针等于队尾指针时,队列为空
}//入队
void enQueue(struct Queue* q,struct TreeNode *node)
{q->data[q->rear]=*node; //将结点指针添加到队列尾部,并将队尾指针+1q->rear++; //队尾指针加一
}//出队
struct TreeNode* deQueue (struct Queue* q)
{return &q->data[q->front++]; //返回队头指针指向的结点指针,并将队头指针+1
}//创建二叉树
struct TreeNode *createTree()
{int val;scanf("%d",&val); //输入结点的值if(val == -1) //如果输入-1,表示该结点为空节点{return NULL;}struct TreeNode *node = (struct TreeNode*)malloc(sizeof(struct TreeNode)); //申请结点空间node->val=val; //赋值node->left = createTree(); //递归创建左子树node->right = createTree(); //递归创建右子树return node;
}//二叉树的层序遍历
void levelOrder(struct TreeNode* root)
{if(root == NULL) //判断是否为空树{return ;}struct Queue q; //定义队列initQueue (&q,100); //初始化队列enQueue(&q,root); //根节点入队while (!isEmpty(&q)) //队列不为空时{struct TreeNode* node = deQueue(&q); //取出队头指针指向的结点指针printf("%d",node->val); //输出结点的值if(node->left != NULL) //如果结点有左子节点将左子节点指针入队{enQueue(&q,node->left);}if (node->right != NULL) { //如果节点有右子节点,将右子节点指针入队enQueue(&q, node->right);}}
}// 测试
int main() {printf("请输入二叉树的节点,-1表示空节点:\n");struct TreeNode *root = createTree(); // 创建二叉树printf("层序遍历结果为:");levelOrder(root); // 二叉树的层序遍历printf("\n");return 0;
}
非递归代码实现
#include
#include // 定义二叉树节点结构体
struct TreeNode {int val; // 节点的值struct TreeNode *left; // 左子节点指针struct TreeNode *right; // 右子节点指针
};// 创建二叉树
struct TreeNode *createTree() {int val;struct TreeNode *root = NULL; // 根节点初始化为空struct TreeNode *curr = NULL; // 当前节点初始化为空struct TreeNode *parent = NULL; // 父节点初始化为空printf("请输入二叉树的节点,-1表示空节点:\n");while (scanf("%d", &val) == 1) { // 循环读入节点的值if (val == -1) { // 如果输入-1,表示该节点为空节点continue;}// 创建节点curr = (struct TreeNode *) malloc(sizeof(struct TreeNode));curr->val = val;curr->left = NULL;curr->right = NULL;// 判断是否为根节点if (root == NULL) {root = curr;} else {parent = root;while (1) { // 在树中查找节点的插入位置if (val < parent->val) {if (parent->left == NULL) {parent->left = curr;break;} else {parent = parent->left;}} else {if (parent->right == NULL) {parent->right = curr;break;} else {parent = parent->right;}}}}}return root; // 返回根节点指针
}// 层序遍历
void levelOrder(struct TreeNode *root) {if (root == NULL) {return;}// 定义一个队列,用于存储待访问的节点struct TreeNode **queue = (struct TreeNode **) malloc(sizeof(struct TreeNode *) * 1000);int front = 0, rear = 0;queue[rear++] = root; // 根节点入队while (front < rear) { // 当队列不为空时struct TreeNode *node = queue[front++]; // 出队一个节点printf("%d ", node->val); // 输出该节点的值if (node->left != NULL) { // 如果该节点有左子节点,将左子节点入队queue[rear++] = node->left;}if (node->right != NULL) { // 如果该节点有右子节点,将右子节点入队queue[rear++] = node->right;}}
}// 测试
int main() {struct TreeNode *root = createTree(); // 创建二叉树printf("层序遍历结果为:");levelOrder(root); // 二叉树的层序遍历printf("\n");return 0;
}
二叉树遍历算法的应用
- 遍历是二叉树各种操作的基础,假设访问结点的具体操作不仅仅局限于输出结点数据域的值,而把访问延伸到对结点的判别、计数等其他操作,可以解决一些关于二叉树的其他实际问题。如果在遍历过程中生成结点,这样便可建立二叉树的存储结构。
先序遍历的顺序创建二叉树
按照先序遍历序列建立二叉树的二叉链表。
例:已知先序序列为:A B C D E G F
- 从键盘中输入二叉树的结点信息,建立二叉树的存储结构。
- 在建立二叉树的过程中按照二叉树先序的方式建立。先建立根节点,然后建立左子树,最后建立右子树
- 只知道先序序列的话,构造的树是不唯一的,下面两种树都有可能。

- 如果想建立的是第一棵树而不是第二棵,可以给这两棵树补充一些空节点,补充完之后这两棵树就不一样了。

- 空节点可以用空格符或者其他符号来表示
- 扫描字符序列,读入字符 ch
- 如果 ch 是一个 # 字符,则表示该二叉树为空树,即 T 为 NULL;否则执行以下操作:
- 申请一个结点空间 T。
- 将输入的字符 ch 符给结点的数据域 T->data。
- 递归创建 T 的左子树。
- 递归创建 T 的右子树。

#include "stdio.h"
#include "stdlib.h"//定义二叉树结点结构体
typedef struct TreeNode {int data ;struct TreeNode* left;struct TreeNode* right;
}TreeNode;//先序遍历顺序简历二叉链表
void createTree(TreeNode** node)
{int data ;scanf("%d",&data );if(data == -1){*node= NULL;}else{//创建新结点*node = (TreeNode*)malloc (sizeof(TreeNode));(*node)->data=data;//递归构建左右子树createTree(&((*node)->left));createTree(&((*node)->right));}
}//先序遍历二叉树
void preOrder(TreeNode* node)
{if(node != NULL){printf("%d",node->data);preOrder(node->left);preOrder(node->right);}
}int main()
{TreeNode* root = NULL;//读取先序遍历序列,构建二叉树printf("请输入先序遍历序列,用-1表示空节点:\n");createTree(&root);//输出二叉树的先序遍历结构printf("二叉树的先序遍历结果为:\n");preOrder(root);return 0;
}
复制二叉树
- 如果要复制的树为空树,则递归结束;
- 否则执行以下操作:
- 申请一个新结点空间,复制根结点。
- 递归复制左子树。
- 递归复制右子树。
#include
#include // 定义二叉树节点结构体
typedef struct node {int data;struct node* left;struct node* right;
} Node;// 创建节点
Node* create_node(int data) {// 分配内存空间Node* new_node = (Node*) malloc(sizeof(Node));// 初始化节点数据new_node->data = data;new_node->left = NULL;new_node->right = NULL;// 返回新节点return new_node;
}// 复制二叉树
Node* clone_tree(Node* root) {// 如果原树为空,则返回空if (root == NULL) {return NULL;} else {// 创建新节点并设置数据Node* new_root = create_node(root->data);// 递归复制左子树new_root->left = clone_tree(root->left);// 递归复制右子树new_root->right = clone_tree(root->right);// 返回新节点return new_root;}
}// 打印二叉树(先序遍历)
void print_tree(Node* root) {if (root != NULL) {// 打印当前节点的数据printf("%d ", root->data);// 递归打印左子树print_tree(root->left);// 递归打印右子树print_tree(root->right);}
}// 主函数
int main() {// 创建一个简单的二叉树Node* root = create_node(1);root->left = create_node(2);root->right = create_node(3);root->left->left = create_node(4);root->left->right = create_node(5);// 打印原始二叉树printf("Original tree: ");print_tree(root);printf("\n");// 复制二叉树Node* cloned_tree = clone_tree(root);// 打印复制的二叉树printf("Cloned tree: ");print_tree(cloned_tree);printf("\n");// 释放内存空间free(root->left->right);free(root->left->left);free(root->right);free(root->left);free(root);free(cloned_tree->left->right);free(cloned_tree->left->left);free(cloned_tree->right);free(cloned_tree->left);free(cloned_tree);return 0;
}/*在这个示例中,我们首先定义了一个Node结构体,表示二叉树的节点。我们使用create_node()函数创建节点,该函数使用给定的数据参数创建新节点,并将左右子节点初始化为NULL。然后,我们定义了clone_tree()函数来复制二叉树。这个函数使用递归的方式实现,首先创建一个新的根节点,并将它的值设置为原始根节点的值。然后,它递归调用clone_tree()函数来复制左右子树,并将它们分别设置为新节点的左右子节点。如果原始根节点为空,则函数返回NULL。最后,我们定义了print_tree()函数来打印二叉树。该函数使用先序遍历的方式打印节点的值。在main()函数中,我们创建了一个简单的二叉树,并使用print_tree()函数打印它。然后,我们使用clone_tree()函数复制该树,并再次使用print_tree()函数打印复制树的内容。*/ 计算二叉树的深度

- 如果是空树,则递归结束,且返回深度为0,反之执行以下操作:
- 递归计算左子树的深度记为 m。
- 递归计算右子树的深度记为 n 。
- 如果 m 大于 n,二叉树的深度为 m + 1,反之为 n + 1,加的这个 1 是根结点的那一层。
#include
#include // 定义二叉树结构体
struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;
};// 计算二叉树的深度
int maxDepth(struct TreeNode* root) {if (root == NULL) { // 当前节点为空,深度为0return 0;}else { // 否则,递归计算左右子树的深度,并取较大值int leftDepth = maxDepth(root->left);int rightDepth = maxDepth(root->right);return (leftDepth > rightDepth) ? (leftDepth + 1) : (rightDepth + 1);}
}int main() {// 创建二叉树struct TreeNode *root = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->val = 1;root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->left->val = 2;root->left->left = NULL;root->left->right = NULL;root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->right->val = 3;root->right->left = NULL;root->right->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->right->right->val = 4;root->right->right->left = NULL;root->right->right->right = NULL;// 计算二叉树深度并输出结果int depth = maxDepth(root);printf("Depth of binary tree is %d\n", depth);return 0;
}/*
在 maxDepth 函数中,我们使用递归的方式计算二叉树的深度,首先判断当前节点是否为空,如果是,则深度为0;否则,递归计算左右子树的深度,并取较大值加1作为当前节点的深度。*/
统计二叉树中结点的个数
-
如果是空树,则结点个数为 0。
-
反之结点个数为:左子树的结点个数 + 右子树的结点个数再 + 1(根节点)。
-
先求左子树的左子树,再加上左子树的右子树,最后加上左子树的根。
如:
- 刚开始时指针是指向根节点 a 的,如果根节点不为空,则去统计它的左子树有多少个结点。
- 以 a 的左孩子结点 b 作为参数再次调用这个函数,
- 此时进入第三层调用,用当前根节点的左孩子 c 来调用这个函数。
- 再次以 c 为根节点调用它的左孩子,发现为空为 0,然后去算c的右子树,发现也为空(0),然后以c为根节点的这个左子树的结点数为 0 + 0 + 1 = 1。

#include
#include // 定义二叉树结构体
struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;
};// 计算二叉树节点总个数
int countNodes(struct TreeNode* root) {if (root == NULL) { // 当前节点为空,节点个数为0return 0;}else { // 否则,递归计算左右子树节点个数,并加上当前节点int leftCount = countNodes(root->left);int rightCount = countNodes(root->right);return leftCount + rightCount + 1;}
}int main() {// 创建二叉树struct TreeNode *root = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->val = 1;root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->left->val = 2;root->left->left = NULL;root->left->right = NULL;root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->right->val = 3;root->right->left = NULL;root->right->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->right->right->val = 4;root->right->right->left = NULL;root->right->right->right = NULL;// 计算二叉树节点总个数并输出结果int count = countNodes(root);printf("Total number of nodes in binary tree is %d\n", count);return 0;
}
计算叶子结点数
#include
#include // 定义二叉树结构体
struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;
};// 计算二叉树中叶子节点数
int countLeaves(struct TreeNode* root) {if (root == NULL) { // 当前节点为空,叶子节点个数为0return 0;}else if (root->left == NULL && root->right == NULL) { // 当前节点没有左右子节点,是叶子节点return 1;}else { // 否则,递归计算左右子树的叶子节点个数,并返回总和int leftCount = countLeaves(root->left);int rightCount = countLeaves(root->right);return leftCount + rightCount;}
}int main() {// 创建二叉树struct TreeNode *root = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->val = 1;root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->left->val = 2;root->left->left = NULL;root->left->right = NULL;root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->right->val = 3;root->right->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->right->left->val = 4;root->right->left->left = NULL;root->right->left->right = NULL;root->right->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->right->right->val = 5;root->right->right->left = NULL;root->right->right->right = NULL;// 计算二叉树中叶子节点数并输出结果int count = countLeaves(root);printf("Total number of leaves in binary tree is %d\n", count);return 0;
}/*
上面的示例中,我们实现了一个名为 countLeaves 的函数,该函数用于计算给定二叉树中叶子节点的总个数。在 countLeaves 函数中,我们使用递归的方式计算二叉树中叶子节点的总个数,首先判断当前节点是否为空,如果是,则叶子节点个数为0;如果当前节点没有左右子节点,即为叶子节点,返回1;否则,递归计算左右子树中叶子节点的总个数,并返回总和。最后,我们在 main 函数中创建了一个二叉树,并调用 countLeaves 函数计算二叉树中叶子节点的总个数并输出结果。
*/
线索二叉树
为什么要研究线索二叉树?
- 当用二叉链表作为二叉树的存储结构时,可以很方便的找到某个结点的左右孩子;
- 但一般情况下,无法直接找到该结点在某种遍历序列中的前趋和后继结点。

提出的问题
- 如何寻找特定(先中后)遍历序列中二叉树结点的前趋和后继?
解决方法
- 通过遍历寻找 — 费时间。
- 给每个结点再增加两个指针域,用来存放该结点的前趋、后继结点 — 增加了存储负担。
- 利用二叉链表中的空指针域

1. 利用二叉链表中的空指针域
- 如果某个结点的左孩子为空,则将空的左孩子指针域改为指向其前趋。如果某结点的右孩子为空,则将空的右孩子指针域改为指向其后继。-
- 这种改变指向的指针称为线索。
- 加上了线索的二叉树称为线索二叉树(Threaded Binary Tree)。
- 对二叉树按某种遍历次序使其变位线索二叉树的过程叫做线索化。
举个栗子
- 有个以下图这棵二叉树为原型存储的二叉链表

- 根节点 A 没有右孩子,又因为 A 属于中序遍历的最后一个结点,它没有后继,所以继续空着。
- B 的左、右孩子指针域不为空,不管。
- C 结点没有左右孩子
- 又发现 C 是中序遍历的第一个结点,没有前趋结点,左孩子域继续为空。
- C 的后继结点是 B,将右孩子域改为指向 B 这个结点。
- D 结点没有空指针域,不管。
- E 没有左孩子,它的前趋是 B 结点,所以将左指针域内的指针改为指向 B 结点。
- F 没有左右孩子,将左指针指向 D 结点,右指针指向 A 结点。
- G 没有左右孩子,左指向 E,右指向 D。

为区分 lrchild 和 rchild 指针到底是指向孩子的指针,还是指针前趋或者后继的指针,对二叉链表中每个结点增加两个标志域 ltag 和 rtag其中:
- 若ltag = 0,则 lchild 指向该结点的左孩子。
- 若ltag = 1,则 lchild 指向该结点的前趋。
- 若rtag = 0,则 rchild 指向该结点的右孩子。
- 若rtag = 1,则 rchild 指向该结点的后继。

//二叉树的二叉线索存储表示
typedef struct BiThrNode
{int data;//数据域,存储数据元素本身int ltag,rtag;//左右标记域,存放 0 1struct BiThrNode* lchild,rchild;//左右孩子指针}BiThrNode,*BiThrTree;
2. 构造线索二叉树
先序线索二叉树
- 存储线索的时候,存储的是它先序遍历下的前趋、后继。

- A 的两个指针分别指向左、右孩子,所以两个标记都是 0.
- B 没有左孩子,所以左孩子域存储 A 的地址,A 是 B 的前趋,所以 ltag为 1。右孩子指针指向的是 B 结点的右孩子 C 结点,所以 rtag为 0。
- C 结点左孩子指针指向前趋 B,ltag为1,右孩子域指向后继 D,所以 rtag 为 1。
- D 结点左孩子域指向 E,E为D的左孩子,所以 ltag为 0,D的右孩子域为空,所以指向D的后继E,rtag 为1.
- E 结点没有左右孩子,左孩子指向前趋D,ltag 为1,又因为E结点既没有右孩子也没用后继,所以右指针为空,且 rtag为1.
有了先序构造线索二叉树之后,中序、后序也是同样的道理。


#include
#include // 定义二叉树结构体
struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;int leftTag; // 左指针标记,0表示指向左子树,1表示指向前驱节点int rightTag; // 右指针标记,0表示指向右子树,1表示指向后继节点
};// 定义全局变量,用于记录最后一个访问的节点
struct TreeNode* lastVisited = NULL;// 对二叉树进行线索化
void createInOrderThread(struct TreeNode* root) {if (root == NULL) {return;}createInOrderThread(root->left); // 递归线索化左子树if (root->left == NULL) { // 如果左子树为空,将左指针标记为1,并指向前驱节点root->leftTag = 1;root->left = lastVisited;}if (lastVisited != NULL && lastVisited->right == NULL) { // 如果前驱节点的右指针为空,将右指针标记为1,并指向后继节点lastVisited->rightTag = 1;lastVisited->right = root;}lastVisited = root; // 更新最后访问的节点createInOrderThread(root->right); // 递归线索化右子树
}// 中序遍历线索化二叉树
void inOrderTraversal(struct TreeNode* root) {struct TreeNode *p = root;while (p != NULL) {while (p->leftTag == 0) { // 找到最左下的节点p = p->left;}printf("%d ", p->val); // 访问节点while (p->rightTag == 1) { // 如果右指针是线索,则遍历后继节点p = p->right;printf("%d ", p->val);}p = p->right; // 否则,遍历右子树}
}
// 释放二叉树的内存
void destroyTree(struct TreeNode* root) {if (root == NULL) {return;}destroyTree(root->left);destroyTree(root->right);free(root);
}//测试
int main() {// 创建线索二叉树struct TreeNode *root = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->val = 4;root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->left->val = 2;root->left->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->left->left->val = 1;root->left->left->left = NULL;root->left->left->right = NULL;root->left->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->left->right->val = 3;root->left->right->left = NULL;root->left->right->right = NULL;root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->right->val = 6;root->right->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->right->left->val = 5;root->right->left->left = NULL;root->right->left->right = NULL;root->right->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));root->right->right->val = 7;root->right->right->left = NULL;root->right->right->right = NULL;// 对二叉树进行中序遍历线索化createInOrderThread(root);// 中序遍历线索化二叉树printf("Inorder traversal of threaded binary tree: ");inOrderTraversal(root);printf("\n");// 释放二叉树内存destroyTree(root);return 0;
} 