0201概述和可达性-有向图-数据结构和算法(Java)
文章目录
- 1 概述
- 2 有向图数据类型
- 2.1 API
- 2.2 数据结构
- 2.3 有向图取反
- 2.4 源代码
- 3 有向图的可达性
- 3.1 概述和API
- 3.2 可达性算法实现
- 3.3 测试
- 3.4 标记-清除的垃圾收集
- 后记
1 概述
- 定义
一幅有向图由一组顶点和一组有方向的边组成,每条有向边有连接着有序的一对顶点。
- 相关概念
有向边:一条有向边由一个顶点指出并指向第二个顶点。
出度:一个顶点的出度为友该顶点指出的边的总数。
入度:一个顶点的入度为指向该顶点的边的总数。
v->w:表示有向图中友顶点v指向w的边。
有向路径:由一系列顶点组成,对于其中的每个顶点都存在一条有向边指向序列中的下一个顶点。
有向环:为一条至少含有一条且顶点和终点相同的有向路径。
简单有向环:上一条(除了起点和终点必须相同外)不含有重复顶点和边的环。
路径或者边的长度:路径或者边所包含的边数。
2 有向图数据类型
2.1 API
有向图API如下表所示:
| public class | Digraph | |
|---|---|---|
| Digraph(int V) | 创建一幅含有V个顶点但不含有边的有向图 | |
| Digraph(In in) | 从输入流中读取一幅有向图 | |
| int | V() | 顶点总数 |
| int | E() | 边的总数 |
| public void | addEdge(int v, int w) | 向有向图中添加一条边v->w |
| public Iterable | adj(itn v) | 友v指出的边所连接的所有顶点 |
| public Digraph | reverse() | 该图的反向图 |
| public String | toString() | 该图的字符串表示 |
2.2 数据结构
有向图使用邻接表表示,边v->w表示顶点v的链接表中包含一个顶点w。这种表示方法和无向图一致,不同的是有向图的邻接表中每条边都只会出现一次。
2.3 有向图取反
A PI中的方法reverse()方法返回该有向图的一个副本,但将其中所有边的方向取反。
2.4 源代码
算法第四版提供的jar包实现源代码如下:
package edu.princeton.cs.algs4;import java.util.NoSuchElementException;/*** 有向图 * 删减部分注释,代码没变* @author Robert Sedgewick* @author Kevin Wayne*/public class Digraph {// 系统换行符private static final String NEWLINE = System.getProperty("line.separator");private final int V; // 顶点总数private int E; // 边的总数private Bag[] adj; // 邻接表数组private int[] indegree; // 出度/*** 初始化有V个顶点但是没有边的有向图** @param V the number of vertices* @throws IllegalArgumentException if {@code V < 0}*/public Digraph(int V) {if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be non-negative");this.V = V;this.E = 0;indegree = new int[V];adj = (Bag[]) new Bag[V];for (int v = 0; v < V; v++) {adj[v] = new Bag();}}/** * 从输入流读取一图幅* @throws IllegalArgumentException if {@code in} is {@code null}* @throws IllegalArgumentException if the endpoints of any edge are not in prescribed range* @throws IllegalArgumentException if the number of vertices or edges is negative* @throws IllegalArgumentException if the input stream is in the wrong format*/public Digraph(In in) {if (in == null) throw new IllegalArgumentException("argument is null");try {this.V = in.readInt();if (V < 0) throw new IllegalArgumentException("number of vertices in a Digraph must be non-negative");indegree = new int[V];adj = (Bag[]) new Bag[V];for (int v = 0; v < V; v++) {adj[v] = new Bag();}int E = in.readInt();if (E < 0) throw new IllegalArgumentException("number of edges in a Digraph must be non-negative");for (int i = 0; i < E; i++) {int v = in.readInt();int w = in.readInt();addEdge(v, w); }}catch (NoSuchElementException e) {throw new IllegalArgumentException("invalid input format in Digraph constructor", e);}}/*** 由一幅已知图构建有向图** @param G the digraph to copy* @throws IllegalArgumentException if {@code G} is {@code null}*/public Digraph(Digraph G) {if (G == null) throw new IllegalArgumentException("argument is null");this.V = G.V();this.E = G.E();if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be non-negative");// update indegreesindegree = new int[V];for (int v = 0; v < V; v++)this.indegree[v] = G.indegree(v);// update adjacency listsadj = (Bag[]) new Bag[V];for (int v = 0; v < V; v++) {adj[v] = new Bag();}for (int v = 0; v < G.V(); v++) {// reverse so that adjacency list is in same order as originalStack reverse = new Stack();for (int w : G.adj[v]) {reverse.push(w);}for (int w : reverse) {adj[v].add(w);}}}/*** 返回顶点总数** @return the number of vertices in this digraph*/public int V() {return V;}/*** 返回边的总数** @return the number of edges in this digraph*/public int E() {return E;}//校验顶点是否在 0 <= v < V范围内private void validateVertex(int v) {if (v < 0 || v >= V)throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));}/*** 添加边v→w** @param v the tail vertex* @param w the head vertex* @throws IllegalArgumentException unless both {@code 0 <= v < V} and {@code 0 <= w < V}*/public void addEdge(int v, int w) {validateVertex(v);validateVertex(w);adj[v].add(w);indegree[w]++;E++;}/*** 由顶点v指出边所连接的所有顶点** @param v the vertex* @return the vertices adjacent from vertex {@code v} in this digraph, as an iterable* @throws IllegalArgumentException unless {@code 0 <= v < V}*/public Iterable adj(int v) {validateVertex(v);return adj[v];}/*** 顶点v的出度** @param v the vertex* @return the outdegree of vertex {@code v} * @throws IllegalArgumentException unless {@code 0 <= v < V}*/public int outdegree(int v) {validateVertex(v);return adj[v].size();}/*** 顶点v的入度** @param v the vertex* @return the indegree of vertex {@code v} * @throws IllegalArgumentException unless {@code 0 <= v < V}*/public int indegree(int v) {validateVertex(v);return indegree[v];}/*** 有向图的所有边取反的反向图** @return the reverse of the digraph*/public Digraph reverse() {Digraph reverse = new Digraph(V);for (int v = 0; v < V; v++) {for (int w : adj(v)) {reverse.addEdge(w, v);}}return reverse;}/*** 有向图的字符串表示*/public String toString() {StringBuilder s = new StringBuilder();s.append(V + " vertices, " + E + " edges " + NEWLINE);for (int v = 0; v < V; v++) {s.append(String.format("%d: ", v));for (int w : adj[v]) {s.append(String.format("%d ", w));}s.append(NEWLINE);}return s.toString();}
}
3 有向图的可达性
3.1 概述和API
单点可达性:给定一幅有向图和一个起点s,是否存在一条从s到给定顶点v的有向路径。
多点可达性:给定一幅图和顶点集合,是否存在一条从集合中的任意顶点到达给定顶点v的有向路径。
有向图的可达性API如下表3.1-1所示:
| public class | DirectedDFS | |
|---|---|---|
| DirectedDFS(Digraph digraph, int s) | 在digraph中找到从s可达的所有顶点 | |
| DirectedDFS(Digraph digraph, Iterable | 在digraph中找到从sources中的所有顶点可达的所有顶点 | |
| public boolean | marked(int v) | v是否从起点s可达 |
3.2 可达性算法实现
非递归实现代码如下:
package com.gaogzhen.datastructure.graph.directed;import com.gaogzhen.datastructure.stack.Stack;
import edu.princeton.cs.algs4.Digraph;
import edu.princeton.cs.algs4.Queue;import java.util.Iterator;/*** 有向图可达性*/
public class DirectedDFS {/*** 标记*/private boolean[] marked;/*** 可达顶点计数*/private int count;/*** 计算从起点s可达的顶点* @param G 有向图* @param s 起点* @throws IllegalArgumentException unless {@code 0 <= s < V}*/public DirectedDFS(Digraph G, int s) {marked = new boolean[G.V()];validateVertex(s);bfs(G, s);}/*** 计算从sources所有顶点可达的所有顶点* @param G 有向图* @param sources 多个起点* @throws IllegalArgumentException if {@code sources} is {@code null}* @throws IllegalArgumentException unless {@code 0 <= s < V}* for each vertex {@code s} in {@code sources}*/public DirectedDFS(Digraph G, Iterable sources) {marked = new boolean[G.V()];validateVertices(sources);for (int v : sources) {if (!marked[v]) {bfs(G, v);}}}/*** 广度优先搜索从地点s可达的所有顶点* @param G 无向图* @param s 起点*/private void bfs(Digraph G, int s) {Queue q = new Queue();marked[s] = true;count++;q.enqueue(s);while (!q.isEmpty()) {int v = q.dequeue();for (int w : G.adj(v)) {if (!marked[w]) {marked[w] = true;count++;q.enqueue(w);}}}}/*** 深度优先计算从起点s可达的所有顶点* @param digraph 有向图* @param s 起点*/private void dfs(Digraph digraph, int s) {// 栈记录搜索路径Stack> path = new Stack<>();if (!marked[s]) {// 起点未标记,标记计数加1// 起点默认没标记,可以不加是否标记判断marked[s] = true;count++;Iterable iterable = digraph.adj(s);Iterator it;if (iterable != null && (it = iterable.iterator()) != null){// 顶点对应的邻接表迭代器存入栈path.push(it);}}while (!path.isEmpty()) {Iterator it = path.pop();int x;while (it.hasNext()) {// 邻接表迭代器有元素,获取元素x = it.next();if (!marked[x]) {// 顶点未被标记,标记计数+1marked[x] = true;count++;if (it.hasNext()) {// 邻接表迭代器有元素重新入栈path.push(it);}// 深度优先原则,当前迭代器入栈,新标记顶点的邻接表迭代器入栈,下次循环优先访问Iterable iterable = digraph.adj(x);if (iterable != null && (it = iterable.iterator()) != null){path.push(it);}break;}}}}/*** 从起点s到顶点v是否可达* @param v 顶点* @return {@code true} if there is a directed path, {@code false} otherwise* @throws IllegalArgumentException unless {@code 0 <= v < V}*/public boolean marked(int v) {validateVertex(v);return marked[v];}/*** 返回从起点可达的所有顶点数量* @return 返回从起点可达的所有顶点数量*/public int count() {return count;}/*** 校验顶点索引v是否在0~V-1之间* @param v 顶点v*/private void validateVertex(int v) {int V = marked.length;if (v < 0 || v >= V) {throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));}}/*** 校验顶点集合* @param vertices 顶点集合*/private void validateVertices(Iterable vertices) {if (vertices == null) {throw new IllegalArgumentException("argument is null");}int V = marked.length;int count = 0;for (Integer v : vertices) {count++;if (v == null) {throw new IllegalArgumentException("vertex is null");}validateVertex(v);}if (count == 0) {throw new IllegalArgumentException("zero vertices");}}
}
- dfs为深度优先搜索实现;bfs为广度优先搜索实现。
- 和无向图处理连通性逻辑一样,这里不做详解,可参考0103深度优先搜索和单点连通-无向图-数据结构和算法(Java)
命题D。在有向图中,深度优先搜索(广度优先搜索)标记由一个集合的顶点可达的所有顶点所需的时间与被标记的所有顶点的出度之和成正比。
3.3 测试
这里只测试单点可达性,多点可达性可以自己测试:
public static void testDirectedDFS() {String path = "H:\\gaogzhen\\java\\projects\\algorithm\\asserts\\tinyDG.txt";In in = new In(path);Digraph graph = new Digraph(in);int s = 0;DirectedDFS directedDFS = new DirectedDFS(graph, s);int t = 5;System.out.println(directedDFS.marked(t));System.out.println(directedDFS.count());
}
tinyDG有向图如下图3.3-1所示:
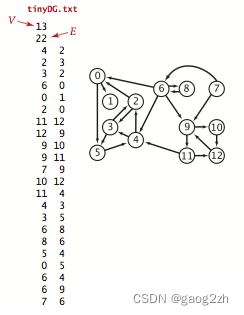
测试结果:
true
6
3.4 标记-清除的垃圾收集
多点可达性一个重要的实际应用是在典型的内存管理系统中,包括许多Java的实现。在一幅有向图中,一个顶点表示一个对象,一条边表示一个对象对另外一个对象的引用。标记-清除的垃圾回收策略会为每个对象保留一位做垃圾搜集使用(Java对象内存模型)。它会周期性的运行一个类似于DirectedDFS的有向图可达性算法来标记所有可以被访问到的对象,然后清理回收没有被标记的对象。
后记
如果小伙伴什么问题或者指教,欢迎交流。
❓QQ:806797785
⭐️源代码仓库地址:https://gitee.com/gaogzhen/algorithm
参考链接:
[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法:第4版[M].北京:人民邮电出版社,2012.10.p364-368.
上一篇:【配电网重构】【SOE】随机配电网重构中的开关开换方法研究(Matlab代码实现)
下一篇:Python安装demjson模块报错:error in demjson setup command: use_2to3 is invalid
