强化学习笔记-04 动态规划Dynamic Programming_学习

强化学习笔记-04 动态规划Dynamic Programming

创始人

2025-05-30 20:23:41

0次

本文是博主对《Reinforcement Learning- An introduction》的阅读笔记，不涉及内容的翻译，主要为个人的理解和思考。

前文介绍的有限马尔可夫决策过程是强化学习建模的基础形式，并介绍了通过Bellman equation的迭代计算可以解决该问题，本文将通过动态规划方法dynamic programming (DP) 来实现这一过程的计算。

当环境建模为有限MDP时，环境中的状态state，动作action和奖励reward的合集是有限的。同时状态间的转换概率p(s’,r|s,a)也是确定的。另外要求状态合集不能太多，因此DP算法本质上会遍历所有的状态，状态数增加会极大增加计算耗时。

1. Generalized Policy Iteration

前文介绍了两阶段迭代计算（Generalized Policy Iteration (GPI)）来完成Bellman equation中的决策函数 $\pi(a|s)$ 和价值函数 v(s) 。这个两阶段的迭代过程分别称之为决策评估Policy Evaluation 和决策优化Policy Improvement。

决策评估Policy Evaluation 是指在特定的决策函数下，去估计各个状态的价值函数，如下的k表示迭代轮数（式1）：

$\\v_{k+1}(s) \\ = \sum_a{\pi(a|s)}E[G_t | s, a] \\ =\sum_a{\pi(a|s)}E[R_t +\gamma G_{t+1} | s, a] \\ =\sum_a{\pi(a|s)}\sum_{s',r}P(s',r|s,a)(r +\gamma v_{k}(s'))$

而决策优化Policy Improvement是指在固定价值函数情况下，确定最优决策函数（式2）

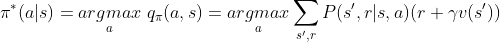
$\\ \pi^{*}(a|s)\\ =\underset{a}{argmax}\ q_{\pi}(a, s)\\ =\underset{a}{argmax} \sum_{s',r} P(s',r|s,a)(r + \gamma v(s'))$

这两阶段的迭代过程会随着训练的加强，最终决策函数和价值函数都会收敛。另外如果我们考虑前文所提到强化学习算法的on-policy和off-policy两种策略，在on-policy中，价值函数可以改写为如下式子（式3），此时价值函数更新时不需要用到决策函数，称这为Value Iteration。

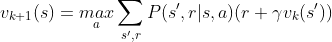
$\\ v_{k+1}(s) =\underset{a}{max} \sum_{s',r}P(s',r|s,a)(r +\gamma v_{k}(s'))$

在更新价值函数时，可以直接用上轮的价值函数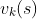 v_k(s) 来更新当前轮 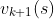$v_{k+1}(s)$ ，另一种是按动态规划的方法，合理安排状态遍历顺序，使得当前状态价值 $s$ 计算所依赖的其他状态 $s'$ 在其之前完成价值函数 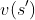v(s') 的计算，此时可以只用一个数组来保存所有的状态价值函数，这种方式可以提升收敛速度。

2. 伪代码实现过程

上述过程的伪代码描述：

3. 例子和代码实现

接下来我们以一个具体的例子实现上述过程：

猜硬币游戏：假设你参加一连续多次的抛硬币猜朝向游戏，在每次抛硬币前，你需要为本次下注一定金额（金额为1~99元之间的整数值），如果硬币朝上，则可以获得下注等额金额，反之则失去下注的金额。这个猜硬币过程可以一直持续进行，直到你手里总共金额达到100元或者0元时结束，假设你刚开始手里有50元，求最优的下注金额。

这个问题我们可以建模为一个有限马尔可夫决策过程，其关键在于状态价值函数 v(s)

当前手里的金额数由状态 $s$ 表示
每次抛硬币前下注金额即为动作 $a$
状态间的转换概率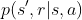可以通过问题背景确定，如下式子中的 $p_h$ 表示硬币朝上的概率，在状态s下选择下注金额后，下一状态只有两种情况：

$p(s',r|s,a)= \begin{cases} 1-p_h & \text{ if } s'=s-a,\ r = -a \\ p_h & \text{ if } s'=s+a,\ r = a \\ 0 & \text{ if } other \\ \end{cases}$

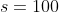价值函数和奖励 $r$ 的表示可以有多种形式，比如可以表示为未来获取的金额，此时奖励 $r$ 则为本轮下注后所赚或输的金额，或者可以表示为最后获胜的概率（最后赢得100元的概率），此时奖励 $r$ 仅当时为1否则为0，如下所示：

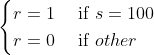
$\begin{cases} r =1& \text{ if } s=100 \\ r=0& \text{ if } other \end{cases}$

决策函数 $\pi(a|s)$ 表示状态s情况下采取动作a的概率，可以用一个表格表示，在初始的情况下，可以用随机选择表示，比如当手里金额为97时，此时下注金额可能为[1,2,3]，假设初始情况下，概率都是一致的。

$\begin{cases} \pi(a|s) = 0 & \text{ if } s=0 \\ \pi(a|s) = 0 & \text{ if } s=100 \\ \pi_0(a|s) = 1/min(100-s, s) & \text{ if } 0< s<100, 0< a < min(100-s, s) \\ \pi_0(a|s) = 0& \text{ if } other \end{cases}$

根据上述的分析，我们很容易写下如下Policy Iteration的代码：

def state_transfers_model(s, a, ph):"""给定状态和动作，返回下一状态、奖励以及转移概率"""r = 0if s + a >= 100:r = 1return [(min(100, s + a), r, ph), (max(0, s - a), 0, 1.0 - ph)]def policy_iteration_dp(is_softmax=False, decay=0.99, det_thred=1e-10, ph=0.4):"""Policy Iteration"""# 1. 初始化V = [0.0 for _ in range(101)]# 决策函数D = [[ 0 for _ in range(100)]]for s in range(1, 100):d = [0]for a in range(1, 100):if a <= min(s, 100 - s):d.append(1/(min(s, 100-s) + 1))else:d.append(0)D.append(d)D.append([0 for _ in range(100)])# Policy IterationD_det = 1000while D_det > det_thred:# 2. Policy EvaluationV_det = 1000while V_det > det_thred:det = 0 # 定义价值函数的变化for s in range(1, 100):before_v = V[s]after_v = 0for a in range(1, min(s, 100 - s) + 1):pa = D[s][a]for next_s, r, p in state_transfers_model(s, a, ph):after_v += pa * p * (r + decay * V[next_s])V[s] = after_vV_det = max(det, abs(after_v - before_v))# 3. Policy ImprovementD_det = 0 # 定义决策函数的变化for s in range(1, 100):q_v = [0]for a in range(1, 100):a_v = 0if a in range(1, min(s, 100 - s) + 1):for next_s, r, p in state_transfers_model(s, a, ph): # q(a, s)a_v += p * (r + decay * V[next_s])q_v.append(a_v)before_Ds = D[s]if is_softmax: # softmax形式设置决策函数after_Ds = list(map(lambda x: x/ sum(q_v), q_v))else: # argmax形式设置决策函数max_a = q_v.index(max(q_v))after_Ds = [0.0] + [0.0] * (max_a - 1) + [1.0] + (99 - max_a) * [0.0]D_det = max(D_det, sum(map(lambda x, y: abs(x - y), before_Ds, after_Ds)))D[s] = after_DsV[100] = 1.0V[0] = 0.0    return V, D

更为简单的Value Iteration的代码：

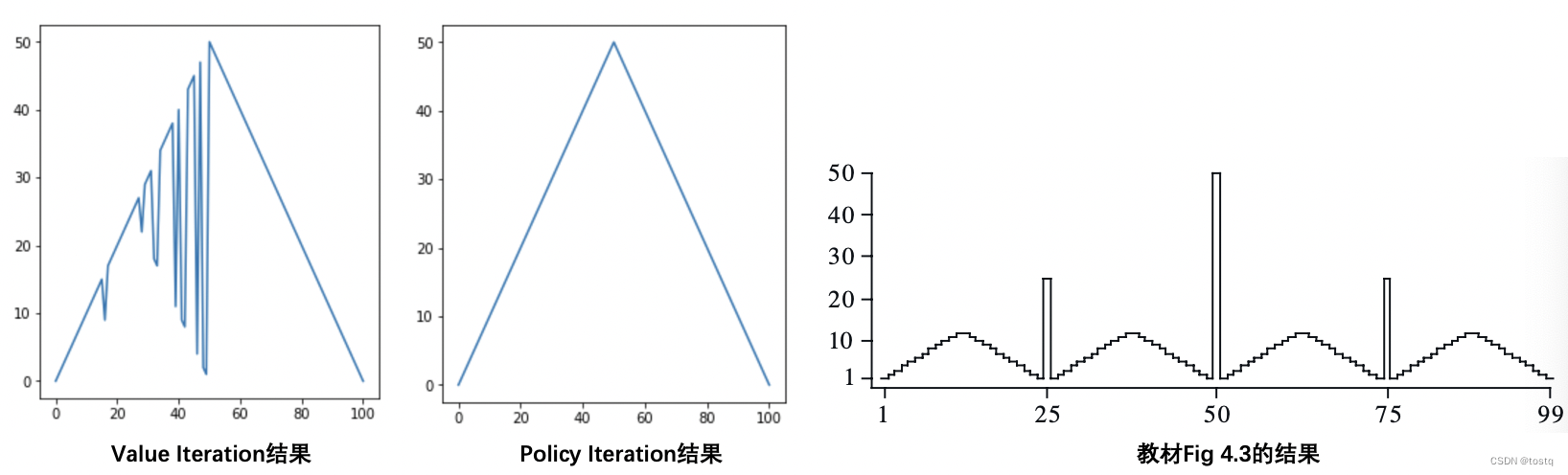
def value_iteration_dp(is_softmax=False, decay=0.99, det_thred=1e-10, ph=0.4):"""Policy Iteration"""# 1. 初始化V = [0.0 for _ in range(101)]# Value Iterationdet = 1000while det > det_thred:det = 0 # 定义价值函数的变化for s in range(1, 100):before_v = V[s]after_vs = []for a in range(1, min(s, 100 - s) + 1):a_v = 0for next_s, r, p in state_transfers_model(s, a, ph):a_v += p * (r + decay * V[next_s])after_vs.append(a_v)after_v = max(after_vs)det = max(det, abs(after_v - before_v))V[s] = after_vD = [[0 for _ in range(100)]] # s=0时无决策for s in range(1, 100):q_v = [0]for a in range(1, 100):a_v = 0if a in range(1, min(s, 100 - s) + 1):for next_s, r, p in state_transfers_model(s, a, ph): # q(a, s)a_v += p * (r + decay * V[next_s])q_v.append(a_v)if is_softmax: # softmax形式设置决策函数Ds = list(map(lambda x: x/ sum(q_v), q_v))else: # argmax形式设置决策函数max_a = q_v.index(max(q_v))Ds = [0.0] + [0.0] * (max_a - 1) + [1.0] + (99 - max_a) * [0.0]D.append(Ds)D.append([0 for _ in range(100)]) # s=100时无决策V[100] = 1.0V[0] = 0.0return V, D

如何读者分别运行上述代码时，会发现每个状态下最优决策动作（下式）是不一样的，而且同教材中的Figure 4.3中的描述的完成不一致（如下图所示），实际上并没有区别，因为这个问题存在无数最优解，只要解的范围在下图中间所示的三角形区域中间即可，具体可以参考作者本人的解释。

$\pi^*(a|s)=\underset{a}{argmax}\ q(s,a)= \underset{a}{argmax}\ D[s][a]$

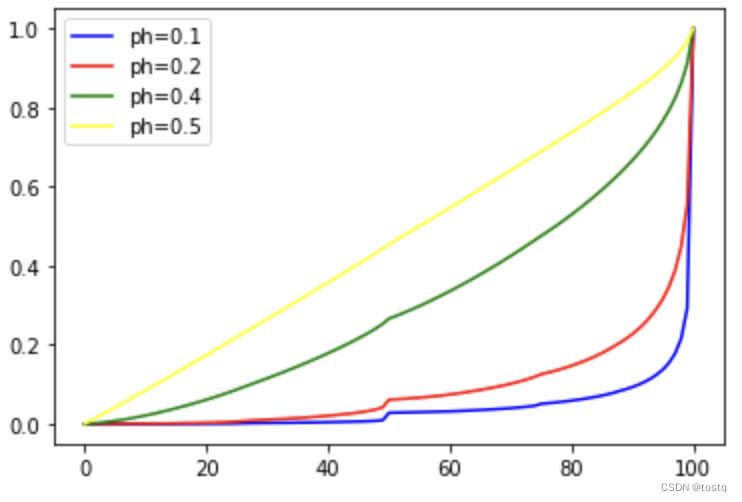
另外我们还发现硬币朝上概率 $p_h$ 的大小实际上并不影响决策函数的分布，其只会影响最终价值函数的分布，如下图：

4. 总结

通过动态规划算法解决了我们第一个强化学习问题，但在现在强化学习中，DP算法很少会用到，因为当状态合集非常庞大时，采用DP算法的耗时非常巨大，虽然可以通过异步DP算法Asynchronous Dynamic Programming，通过分布式的不同的计算节点可以独立地更新价值函数，同时每次更新并不需要计算全部的节点，这种策略可以在一定程度提升计算效率，但这种方式实际上是低效的，特别是当状态是连续的情况，DP算法很难有办法完整解决。

虽然在现在强化学习中，DP算法是过时，但对于我们理解强化学习算法很重要，特别是Generalized Policy Iteration的思想可以帮助我们理解诸如value-base相关的强化学习模型。此外对于环境可知（即状态间的转换概率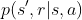 p(s',r|s,a) 是确定的）且状态有限的情况下，DP算法不失是一种非常可靠的选择。

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：寒露微信祝福语和手机短信祝福大全寒露微信祝福语和手机短信祝福大全

下一篇：寒露的祝福语和祝福短信搞笑幽默寒露的祝福语大全冬至幽默搞笑祝福语

强化学习笔记-04 动态规划Dynamic Programming

1. Generalized Policy Iteration

2. 伪代码实现过程

3. 例子和代码实现

4. 总结

相关内容

热门资讯