Chapter2.3：线性表的链式表示
创始人
2025-05-30 10:41:05
0次

该系列属于计算机基础系列中的《数据结构基础》子系列，参考书《数据结构考研复习指导》(王道论坛 组编)，完整内容请阅读原书。

3.线性表的链式表示

3.1 单链表的定义

  • 顺序表可以随时存取表中的任意一个元素，其存储位置可以用一个简单的公式表示，但插入和删除操作需要移动大量的元素；

  • 链式存储线性表，不需要使用地址连续的存储单元，即不要求逻辑上相邻的元素在物理位置上相邻，通过"链"建立起数据元素间的逻辑关系，因此，插入和删除元素不需要移动元素，只需要修改指针，但会失去顺序表可随机存取的优点；

  • 线性表的链式存储亦称单链表，指通过一组任意的存储单元来存储线性表中的数据元素；

  • 为了建立数据元素间的线性关系，对每个链表结点，除存放数据元素本身的信息外，还需要存放一个指向其后继的指针；

  • 单链表结点包括数据域(data)({\rm data})(data)和指针域(next)({\rm next})(next)，数据域存放数据元素，指针域存放后继结点的地址；

  • 单链表的结点类型描述：

    // 定义单链表结点类型
typedef struct LNode{ElemType data;			// 数据域struct LNode *next;		// 指针域
}LNode,*LinkList;

  • 单链表可以解决顺序表需要大量连续存储单元的缺点，但单链表附加指针域，存在浪费存储空间的缺点；

  • 单链表的元素离散地分布在存储空间中，故单链表是非随机存取的存储结构，即不能直接找到表中某个特定的结点；单链表中查找某个特定的结点时，需要从表头开始遍历，依次查找；

  • 通常用头指针来标识一个单链表，如单链表LLL，头指针为NULL{\rm NULL}NULL时表示一个空表；

  • 为了操作上的方便，在单链表第一个结点前附加一个结点，称为头结点；头节点的数据域可不设任何信息，亦可记录表长等信息；头结点的指针域指向线性表的第一个元素结点；

  • 带头结点的单链表表示：

    1

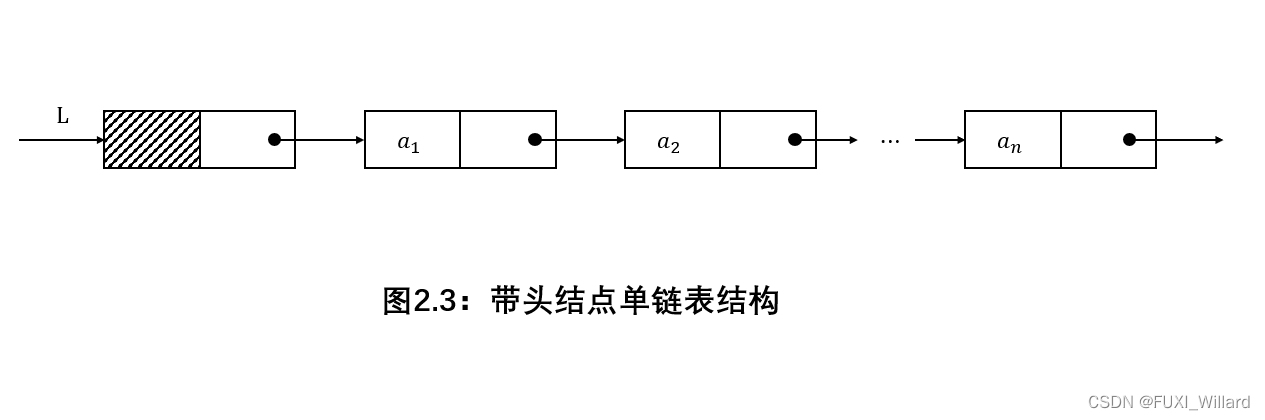
  • 头结点和头指针区分：不管带不带头结点，头指针始终指向链表的第一个结点，头结点是带头结点的链表中的第一个结点，结点内通常不存储信息；

  • 引入头结点的优点：

    • 由于第一个数据结点的位置被存放在头结点的指针域，因此，在链表的第一个位置上的操作和在表的其他位置上的操作一致，无须进行特殊处理；
    • 无论链表是否为空，其头指针都指向头结点的非空指针，空表中头结点的指针域为空，因此，空表和非空表的处理得到统一；
3.2 单链表上基本操作的实现
3.2.1 头插法建立单链表

  • 头插法从一个空表开始，生成新结点，将读取到的数据存放到新结点的数据域中，然后将新结点插入到当前链表的表头，即头结点后；

  • 头插法建立单链表图解：

    2

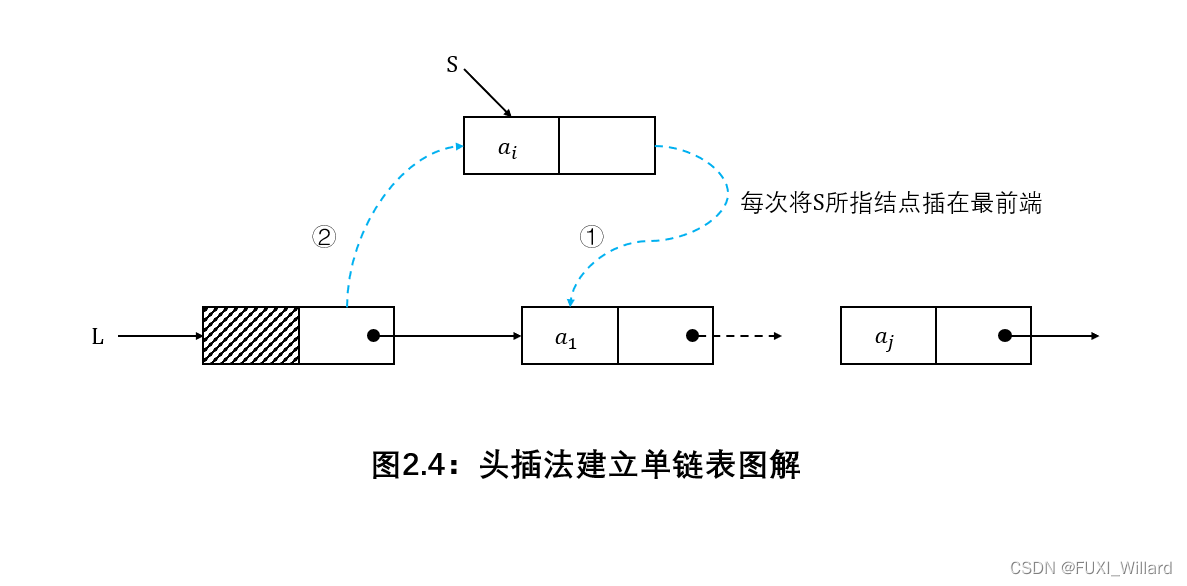
  • 头插法建立单链表算法核心代码：

    // 逆向建立单链表
LinkList List_HeadInsert(LinkList &L){LNode *s;int x;// 创建头结点L=(LinkList) malloc(sizeof(LNode));// 初始化为空链表L->next=NULL;// 输入结点的值scanf("%d",&x);while(x!=9999){// 由系统生成一个LNode型结点，同时将该结点的起始位置赋给指针变量ss=(LNode*) malloc(sizeof(LNode));s->data=x;s->next=L->next;L->next=s;		// 将新结点插入表中，L为头指针scanf("%d",&x);}return L;
}

  • 采用头插法建立单链表，读入数据的顺序与生成的链表中元素的顺序相反；

  • 每个结点插入的时间为O(1)O(1)O(1)，设单链表表长nnn，则总时间复杂度为O(n)O(n)O(n)；

3.2.2 尾插法建立单链表

  • 尾插法将新结点插入到当前链表的表尾，需要增加一个尾指针r{\rm r}r，始终指向当前链表的尾结点；

  • 尾插法建立单链表图解：

    3

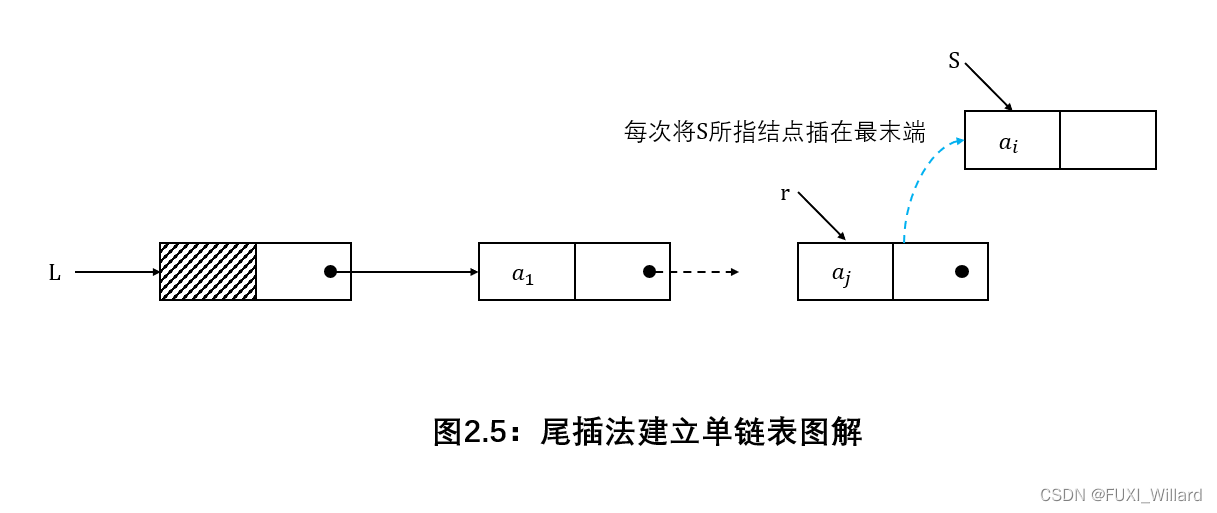
  • 尾插法建立单链表算法核心代码：

    // 正向建立单链表
LinkList List_TailInsert(LinkList &L){int x;				// 元素类型为整型L=(LinkList)malloc(sizeof(LNode));LNode *s,*r=L;		// r为表尾指针scanf("%d",&x);		// 输入结点的值while(x != 9999){s=(LNode *)malloc(sizeof(LNode));s->data=x;r->next=s;r=s;			// s指向新的表尾结点scanf("%d",&x);}r->next=NULL;return L;
}
3.2.3 按序号查找结点值

  • 在单链表中，从第一个结点出发，顺指针next{\rm next}next域逐个往下搜索，直到找到第i{\rm i}i个结点为止，否则返回最后一个结点指针域NULL{\rm NULL}NULL；

  • 按序号查找结点值算法核心代码：

    LNode *GetElem(LinkList L,int i){int j=1;LNode *p=L->next;		// 头结点指针赋给p// 若i等于0，返回头结点if(i == 0)return L;// 若i无效，返回NULLif(i < 1)return NULL;// 查找第i个结点while(p && j < i){p=p->next;j++;}return p;
}

  • 按序号查找操作时间复杂度为O(n)O(n)O(n)；

3.2.4 按值查找表结点

  • 从单链表第一个结点开始，由前往后依次比较表中各结点数据域的值，若某结点数据域的值等于给定值e{\rm e}e，则返回该结点的指针；若整个单链表中没有这样的结点，则返回NULL{\rm NULL}NULL；

  • 按值查找表结点算法核心代码：

    LNode *LocateElem(LinkList L,ElemType e){LNode *p=L->next;// 查找data域为e的结点while(p!=NULL && p->data!=e)p=p->next;return p;
}

  • 按值查找操作时间复杂度为O(n)O(n)O(n)；

3.2.5 插入结点操作

  • 插入结点操作：将值为x{\rm x}x的新结点插入到第i{\rm i}i个位置上；先检查插入位置的合法性，然后找到待插入位置的前驱结点，即第i−1{\rm i-1}i−1个结点，再在其后插入新结点；

  • 算法过程：先调用按序号查找算法GetElem(L,i−1){\rm GetElem(L,i-1)}GetElem(L,i−1)，查找第i−1{\rm i-1}i−1个结点；假设返回的第i−1{\rm i-1}i−1个结点为∗p{\rm *p}∗p,然后令新结点∗s{\rm *s}∗s的指针域指向∗p{\rm *p}∗p的后继结点，再令结点∗p{\rm *p}∗p的指针域指向新插入的结点∗s{\rm *s}∗s；

  • 单链表插入结点操作图解：

    5

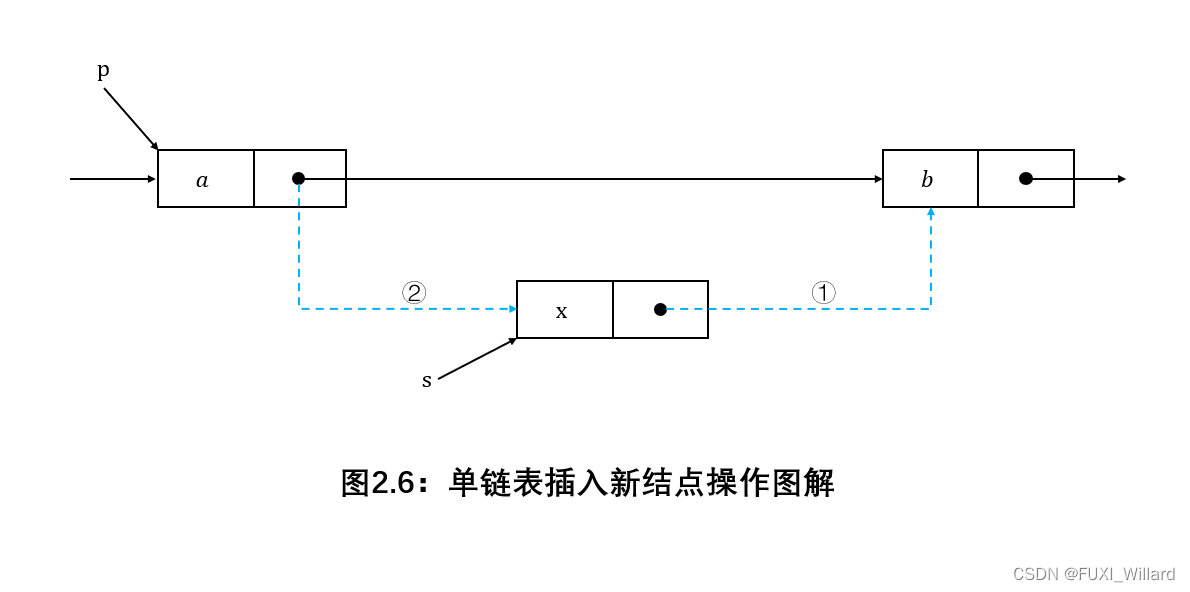
  • 单链表插入新结点操作核心代码：

    // STEP1：查找插入位置的前驱结点
p=GetElem(L,i-1);// STEP2：将新结点s指针域指向p后继结点
s->next=p->next;// STEP3：将结点p的指针域指向新结点s
p->next=s;

  • 单链表插入新结点操作时间复杂度分析：

    该插入新结点操作主要时间开销在于查找第i−1{\rm i-1}i−1个元素，时间复杂度为O(n)O(n)O(n)；若在给定的结点后插入新结点，时间复杂度为O(1)O(1)O(1)；

3.2.6 删除结点操作

  • 删除结点操作：将单链表的第i{\rm i}i个结点删除；

  • 算法思想：先检查删除位置的合法性，后查找表中第i−1{\rm i-1}i−1个结点，即被删除结点的前驱结点，将其删除；

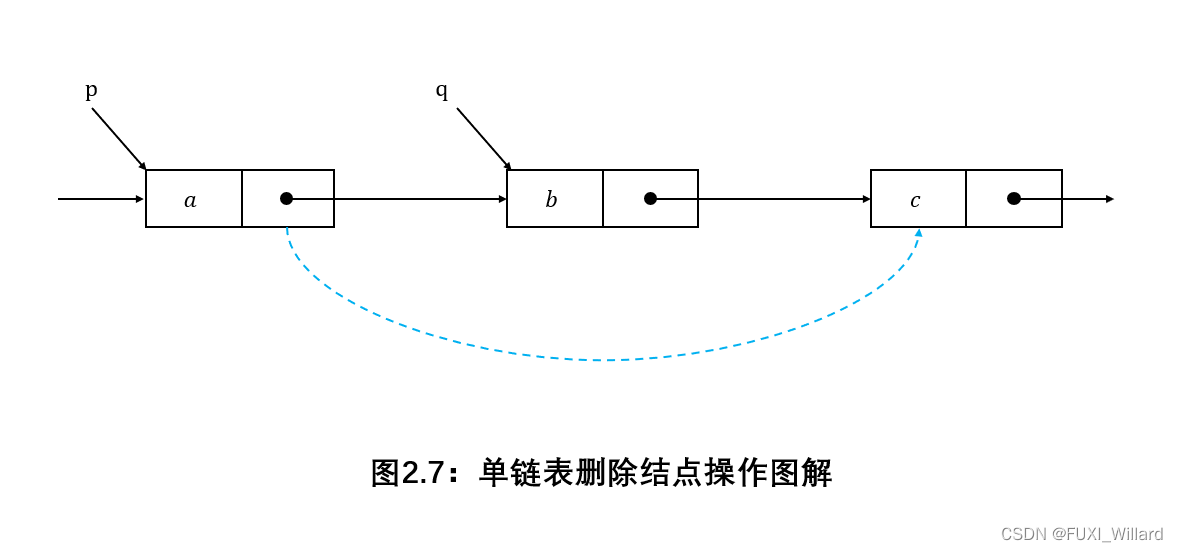
  • 单链表删除结点操作图解：

    6

  • 单链表删除结点操作核心代码：

    // STEP1：查找删除位置的前驱结点
p=GetElem(L,i-1);// STEP2：令q指向被删除结点
q=p->next;// STEP3：将*q结点从单链表中断开
p->next=q->next;// STEP4：释放结点的存储空间
free(q);

  • 单链表删除结点操作时间复杂度分析：

    单链表删除结点操作主要时间耗费在查找操作上，时间复杂度为O(n)O(n)O(n)；

3.2.7 求表长操作
  • 求表长操作：计算单链表中数据结点(不含头结点)的个数；
  • 算法思想：从第一个结点开始顺序依次访问表中每个结点，需要设置一个计数器变量，每访问一个结点，计数器加111，直到访问到空结点为止；
  • 求表长操作时间复杂度为O(n)O(n)O(n)；
3.3 双链表
3.3.1 双链表定义

  • 双链表结点中有两个指针：prior{\rm prior}prior和next{\rm next}next，分别指向其前驱结点和后继结点；

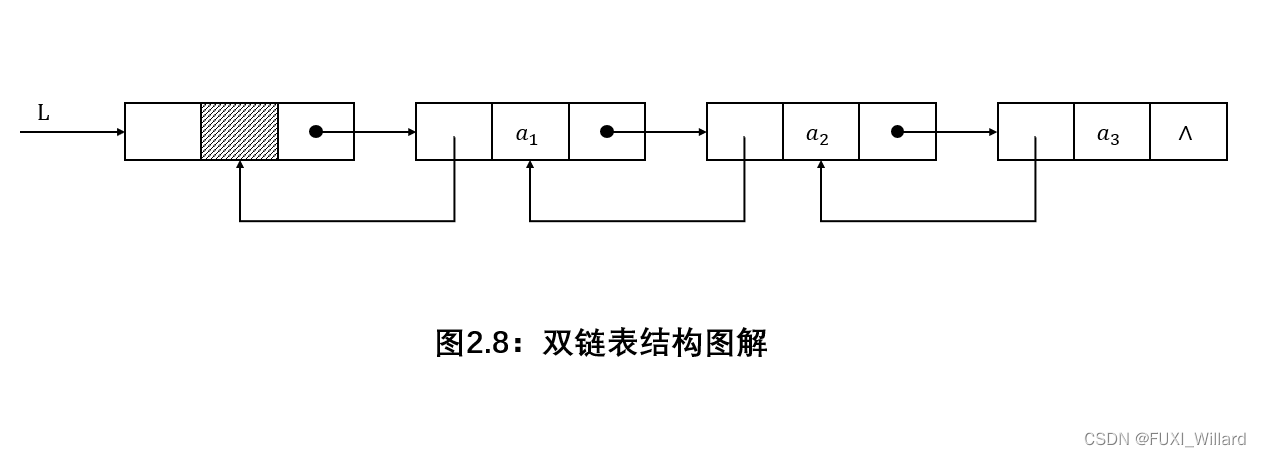
  • 双链表图解：

    7

  • 双链表结点类型描述：

    // 定义双链表结点类型
typedef struct DNode{	ElemType data;					// 数据域struct DNode *prior,*next;		// 结点前驱和后继指针
}DNode,*DLinklist;

  • 双链表在单链表结点中增加一个指向其前驱的prior{\rm prior}prior指针，故双链表中的按值查找和按位查找的操作与单链表相同；

  • 双链表的插入和删除结点操作和单链表操作不同，且双链表插入和删除操作的时间复杂度为O(1)O(1)O(1)；

3.3.2 双链表的插入操作

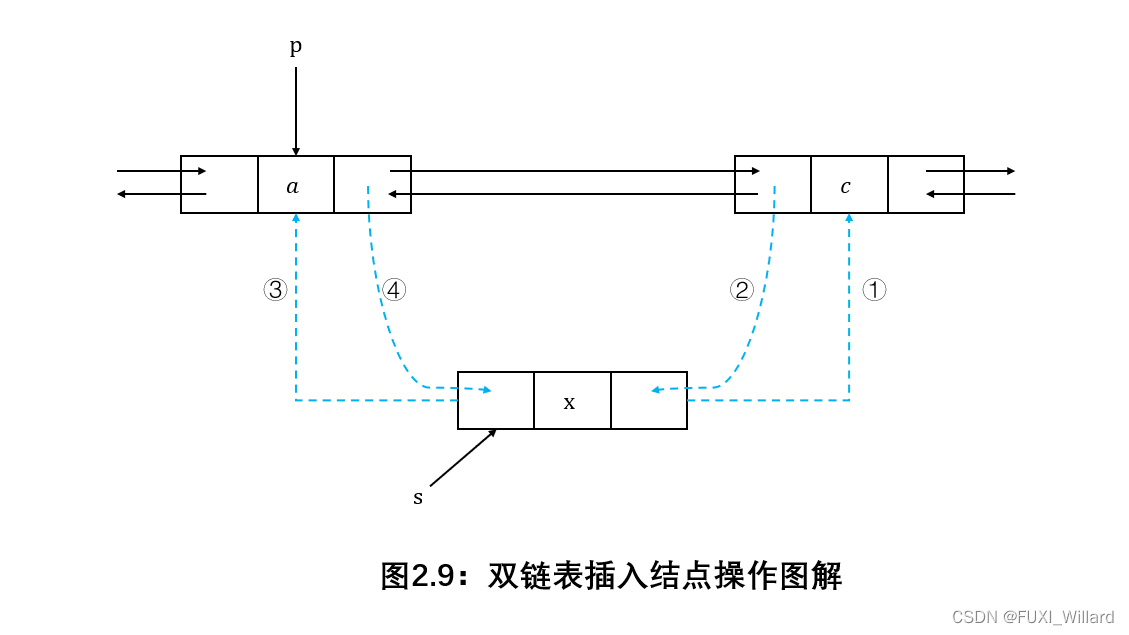
  • 双链表中p{\rm p}p所指结点后插入结点∗s{\rm *s}∗s，插入过程图解如下：

    8

  • 双链表插入结点操作核心代码：

    // 将结点*s插入到结点*p后
s->next=p->next;
p->next->prior=s;
s->prior=p;
p->next=s;
3.3.3 双链表的删除操作

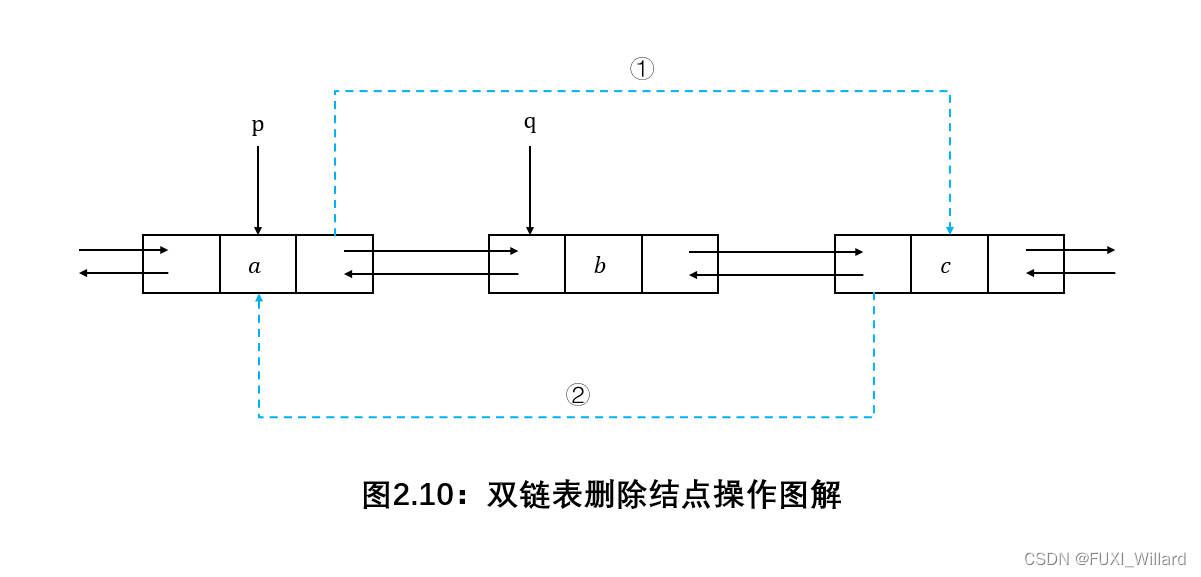
  • 删除双链表结点∗p{\rm *p}∗p的后继结点∗q{\rm *q}∗q，删除过程图解如下：

    9

  • 双链表删除结点操作核心代码：

    // 双链表删除结点
p->next=q->next;
q->next->prior=p;
free(q);				// 释放结点q的空间
3.4 循环链表
3.4.1 循环单链表

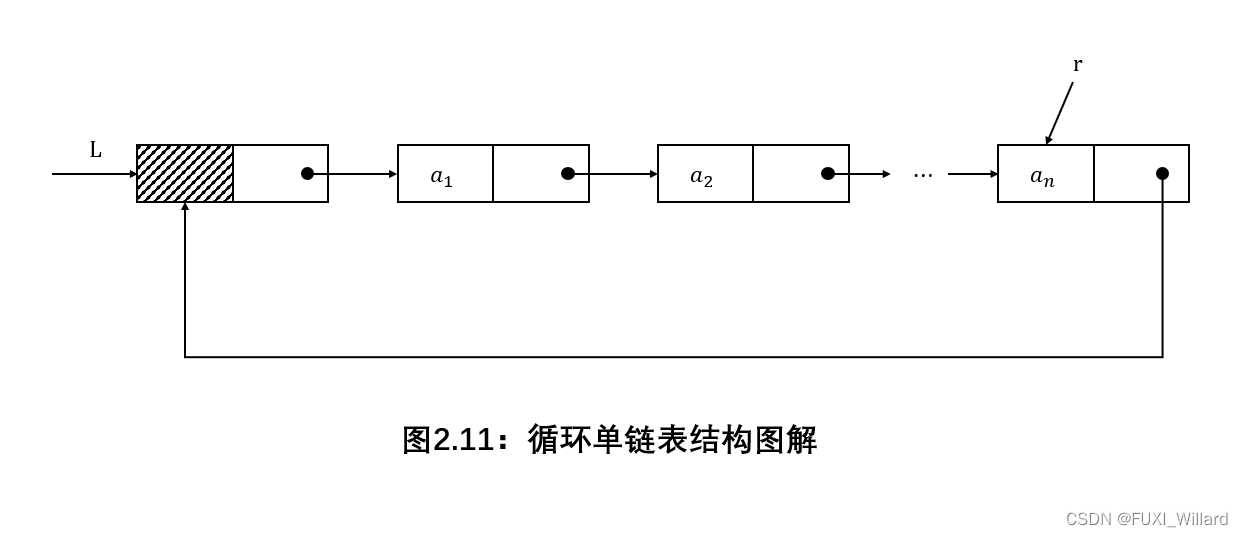
  • 循环单链表最后一个结点的指针不是NULL{\rm NULL}NULL，而是指向头结点，整个链表形成一个环；

  • 循环单链表结构图解如下：

    10

  • 循环单链表中，表尾结点∗r{\rm *r}∗r的next{\rm next}next域指向L{\rm L}L，故表中没有指针域为NULL{\rm NULL}NULL，因此，循环单链表的判空条件不是头结点的指针是否为空，而是是否等于头指针；

3.4.2 循环双链表

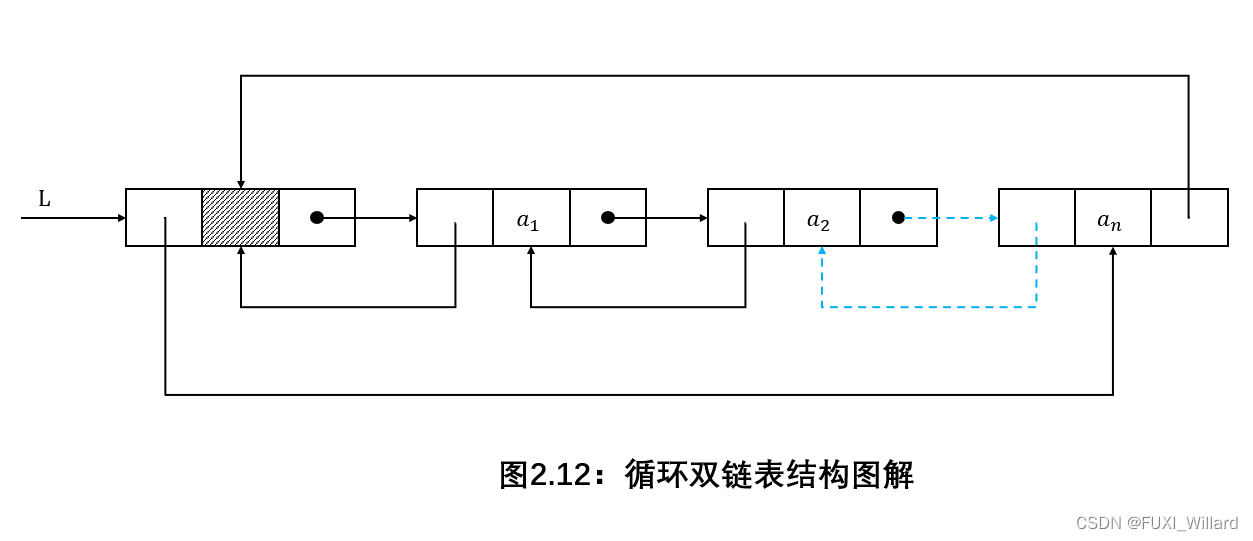
  • 循环双链表中，头结点的prior{\rm prior}prior指针需要指向表尾结点；

  • 循环双链表结构图解如下：

    11

  • 在循环双链表L{\rm L}L中，某结点∗p{\rm *p}∗p为尾结点时，p−>next==L{\rm p->next==L}p−>next==L；当循环双链表为空表时，头结点的prior{\rm prior}prior域和next{\rm next}next域都等于L{\rm L}L；

3.5 静态链表

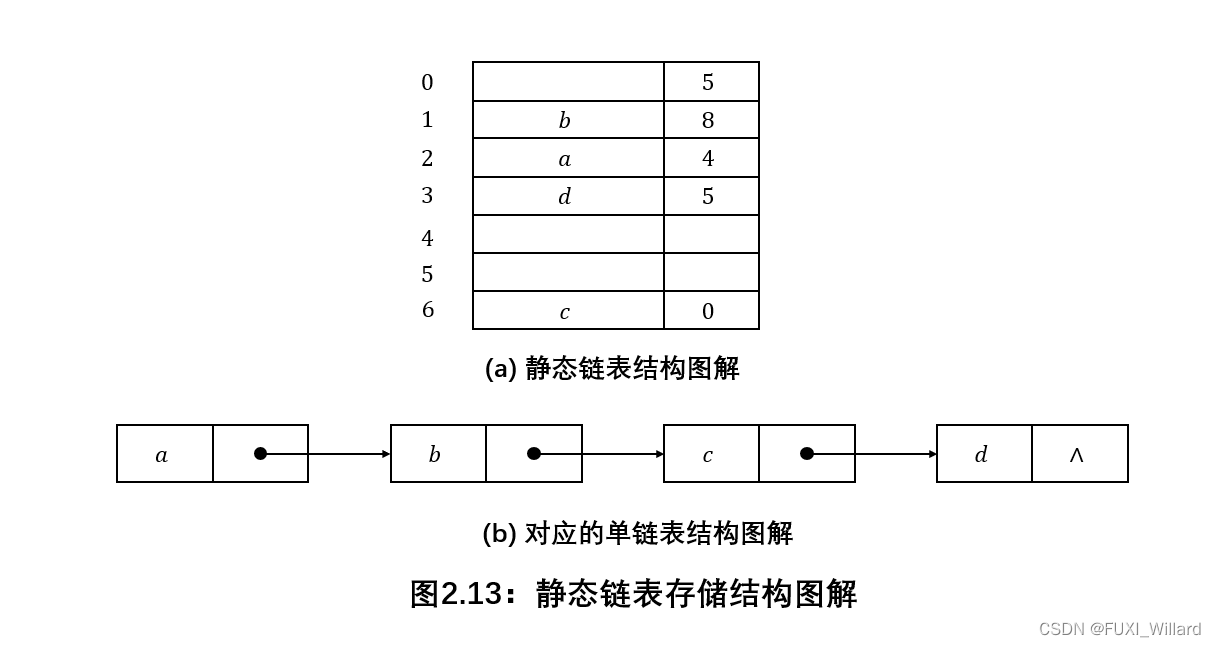
  • 静态链表借助数组描述线性表的链式存储结构，结点也包括数据域data{\rm data}data和指针域next{\rm next}next；

  • 静态链表的指针是结点的相对地址(数组下标)，亦称游标，静态链表亦要预先分配一块连续的内存空间；

  • 静态链表和单链表结构对应关系如下：

    13

  • 静态链表结构类型描述：

    #define MaxSize 50			// 静态链表的最大长度
typedef struct{				// 静态链表结构类型的定义ElemType data;			// 存储数据元素int next;				// 下一个元素的数组下标
}SLinkList[MaxSize];

  • 静态链表以next==−1{\rm next==-1}next==−1作为结束标志，静态链表插入、删除操作与动态链表相同，只需要修改指针，不需要移动元素；

3.6 顺序表和链表比较
3.6.1 顺序表和链表比较
  • 存取(读写)方式。
    • 顺序表可以顺序存取，亦可随机存取；链表只能从表头顺序存取元素；
  • 逻辑结构与物理结构。
    • 顺序存储时，逻辑上相邻的元素，对应的物理存储位置亦相邻；
    • 链式存储时，逻辑上相邻的元素，物理位置不一定相邻，对应的逻辑关系通过指针链接表示；
  • 查找、插入和删除操作。
    • 对于按值查找，顺序表无序时，顺序表和链表的时间复杂度均为O(n)O(n)O(n)；顺序表有序时，采用折半查找，时间复杂度为O(log⁡2n)O(\log_2n)O(log2​n)；
    • 对于按序号查找，顺序表支持随机访问，时间复杂度为O(1)O(1)O(1)；链表平均复杂度为O(n)O(n)O(n)；
    • 顺序表的插入、删除操作，平均需要移动半个表长的元素；链表的插入、删除操作，只需要修改相关结点的指针域即可；链表的每个结点都带有指针域，故存储密度不够大；
  • 空间分配。
    • 顺序存储在静态存储分配情形下，一旦存储空间装满就不能扩充，若再加入新元素，则会出现内存溢出，因此，需要预先分配足够大的存储空间；
    • 顺序存储预先分配存储空间过大，可能会导致顺序表后部大量闲置；顺序存储预先分配存储空间过小，可能造成溢出；
    • 顺序动态存储的存储空间可以扩充，但需要移动大量元素，导致操作效率降低，且若内存没有更大块的连续存储空间，则会导致分配失败；
    • 链式存储的结点空间只在需要时申请分配，只要内存有空间就可以分配，操作灵活、高效；
3.6.2 选取存储结构方法
  • 基于存储的考虑。
    • 难以估计线性表的长度或存储规模时，不宜采用顺序表；
    • 链表不用预先估计存储规模，但链表的存储密度较低，链表的存储密度是小于111的；
  • 基于运算的考虑。
    • 顺序表中按序号访问aia_iai​的时间复杂度为O(1)O(1)O(1)，链表中按序号访问的时间复杂度为O(n)O(n)O(n)，若经常做的运算是按序号访问数据元素，则顺序表优于链表；
    • 顺序表中插入、删除操作时，平均移动表中一半元素，当数据元素信息量较大且表较长时，对此不能忽视；
    • 链表中进行插入、删除操作时，主要是比较操作，从该角度考虑，优于顺序表；
  • 基于环境的考虑。
    • 顺序表容易实现，链表的操作基于指针，有一些语言没有指针类型；
词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：最新或2023（历届）初中生法制手抄报的格式样板 初中法制手抄报模板简单又好看 法制手抄报内容2023年50字

下一篇：2022湖北省赛 L 裸线段树

相关内容

热门资讯

俞敏洪：家庭教育的灵魂是人品教... 我之所以能够在这谈谈家庭教育的心得，确实是因为我接触的孩子太多了。我看到过很多幸福的学生，也看到了很...
汕尾最新学区划分,最新或202... 汕尾公办小学招生范围按照义务教育免试就近入学原则，市区公办小学实行依街道划片招生。本文为您介绍汕尾小...
让老人带孩子到底好不好？如何打... 年轻父母忙于工作，无暇照顾孩子，越来越多的家庭成了隔代教育家庭。那么让老人来带孩子到底好不好？究竟该...
Oracle目录应急清理 Oracle目录应急清理清理错误位置的归档日志清理30天前的监听告警日志清理监听日志清理30天以前的...
最新或2023（历届）小升初作... 著名教育家苏霍姆林斯基说过：“应该让孩子生活在书籍的世界里”。北大资深教授钱理群先生：“学好语文有很...
光电器件——光电半导体器件简介... 首先我们进入光电器件的简介 主要由三五族来形成无机光电半导体 我们用二六族来形成的话，...
9、Cascaded Diff... 简介 主页：https://cascaded-diffusion.github.io/...
央视首推情感教育纪录片《镜子》... （4月19日）晚，央视纪录片《镜子》首播，给了中国家庭教育当头一棒。　　之所以取名“镜子”，是因为“...
朱泾二小：满足孩子与家长的幸福... 教育工作要以孩子和家长“幸福”为追求，满足了学生个性化发展的需求，满足了家长自我提高的需求，家校共同...
争做模范好家长 共育家教新篇章... 为发现和宣传在家庭教育方面有创新有实效的好家长，以及关心教育，支持学校、班级工作的“好家长”先进典型...
比起富养孩子，培养孩子的抗挫商... 1去年十一月，安徽电视台记者段丹峰为情跳楼自杀。自杀前曾连发五小时微博，可见那段时间内她内心遭受多么...
蒙山中学：爆棚的“创城力” 蒙... 家校携手共创城4月27日上午，“我为创城 文明家校”金山区中学家校工作座谈会在蒙山中学举行，来自全区...
Notion汉化 市面上笔记软件五花八门，都各有特色。wolai、语雀、飞书、印象笔记、石墨、幕布、为知...
最新或2023（历届）5月20... 我们用全部的爱关爱家人，我们期待孩子健康快乐的长大，我们竭尽所有把最好的给孩子！每一个小天使的降临，...
最新或2023（历届）.5.9... 亲爱的家人朋友们：欢迎您来到美丽的杭州，参加最新或2023（历届）5月9日—5月11日（周二至周四）...
孩子写作业总是拖拖拉拉？家庭教... 成就孩子美好人生！上城区学生成长支持中心第三讲“督促孩子完成作业的窍门 ”，欢迎家长朋友通过微信报名...
反腐正剧《人民的名义》，是一部... 《人民的名义》自最新或2023（历届）3月28日开播以来，已接近一个月，热度不减，而据CSM52城市...
Spring Boot 自定义... 概述 因为最近一直在为公司搭建底层框架， 好久没有更新博客了,本次搭建的框架结构...
想提升宝宝情商，家庭教育很关键... 爸爸妈妈们，你们是否有过对于如何培养宝宝情商的问题的犯难?可能我们可以给宝宝上最好的学校，或者根据宝...
Redis(九)：并发问题 前言 上一篇介绍了 Redis 的内存管理。这节开始介绍 Redis 并发方面的问题。 Redis ...