目录

0、前言

1、二叉树链式结构的创建

2、二叉树的遍历

3、 前序、中序以及后序遍历

4、 前序、中序以及后序遍历的实现——双路递归

分治思想

 求叶子节点数量，分治思想：

分治思想

求第k层节点个数：

​编辑

分治思想

求二叉树的深度：

分治思想

二叉树查找值为x的结点：

5、二叉树基础oj练习

1. 单值二叉树。

2、检查两颗树是否相同。

3. 对称二叉树。

4. 二叉树的前序遍历。

5. 二叉树中序遍历 。

6. 二叉树的后序遍历 。

7. 另一颗树的子树。

0、前言

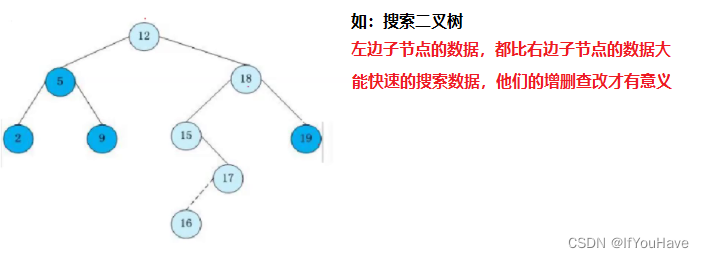
普通二叉树的增删查改没有什么意义，主要学习遍历、结构

而存储数据，不如用顺序表，链表，那么学习他的意义是为了什么？

1.为了后面学习更为复杂的二叉树打基础。（搜索二叉树、ALV树、红黑树、B树、B+树、B*树）

2.有很多二叉树的OJ算法题，都是出在普通二叉树上。

1、二叉树链式结构的创建

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，反过头再来研究二叉树真正的创建方式。

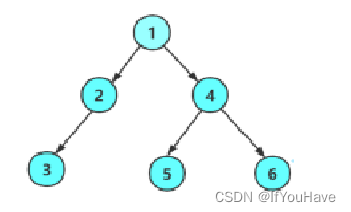
 手搓上图二叉树的链式结构:

typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//手搓二叉树
BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));assert(node);node->data = x;node->left = NULL;node->right = NULL;return node;
}
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}
int main()
{BTNode* root = CreatBinaryTree();return 0;
}

2、二叉树的遍历

学习二叉树结构，最简单的方式就是遍历。

所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉 树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。

遍历 是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

3、 前序、中序以及后序遍历

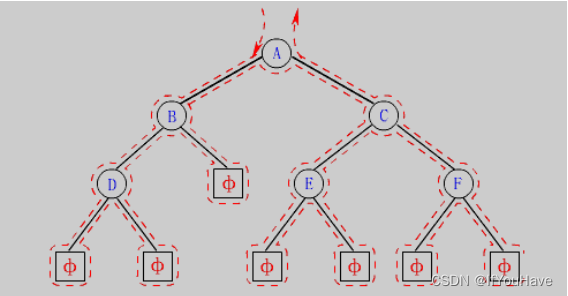
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

1.  前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2.  中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
3.  后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为 根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

4、 前序、中序以及后序遍历的实现——双路递归

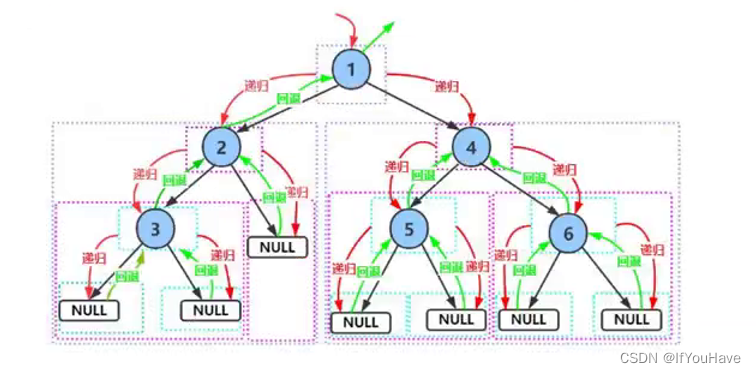
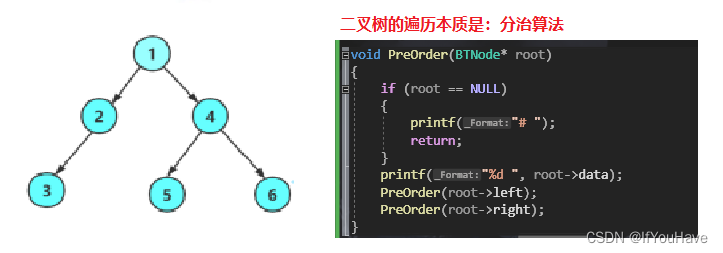
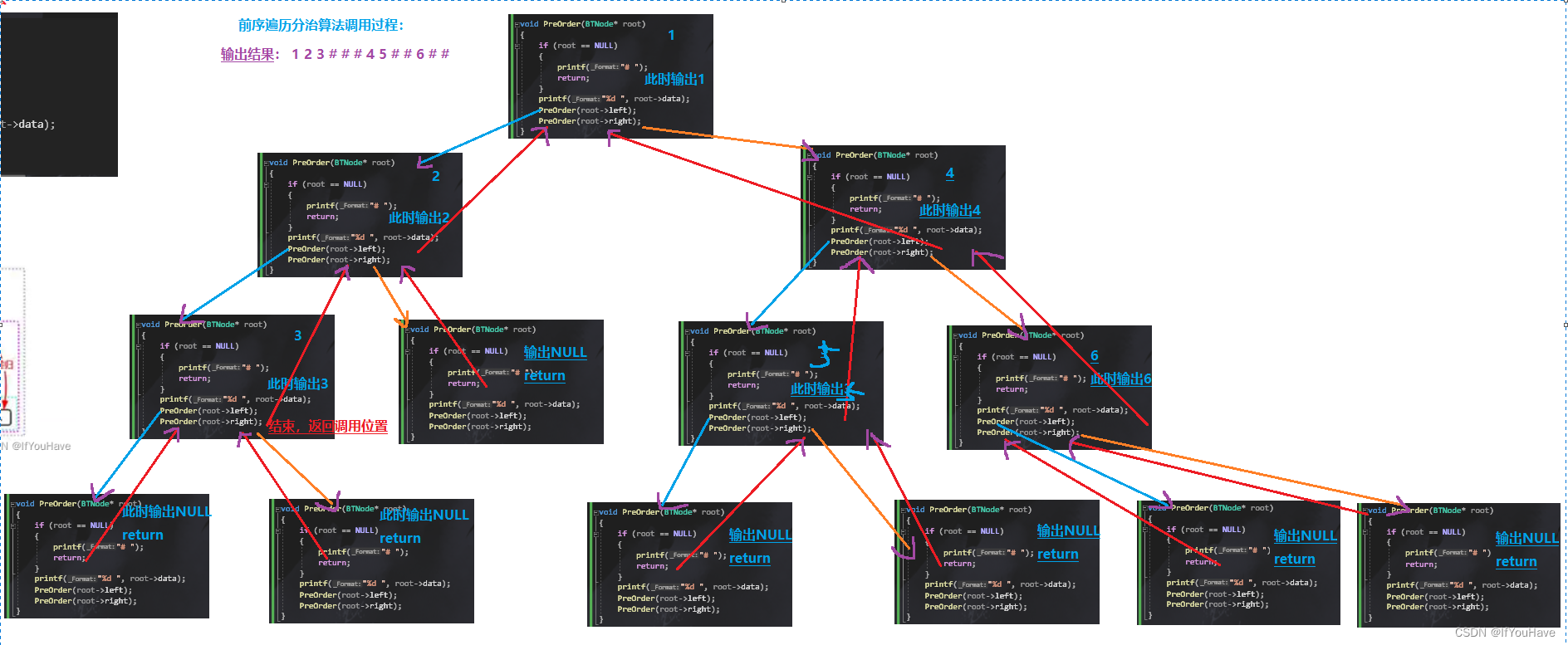
// 二叉树前序遍历
void PreOrder(BTNode * root);
// 二叉树中序遍历
void InOrder(BTNode* root);
// 二叉树后序遍历
void PostOrder(BTNode* root);//求树的数据个数
void TreeSize1(BTNode* root);//解决TreeSize1的问题，分治算法求Size
int TreeSize2(BTNode* root);

#include"BinaryTree.h"BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));assert(node);node->data = x;node->left = NULL;node->right = NULL;return node;
}
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}void PreOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}void InOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}PreOrder(root->left);printf("%d ", root->data);PreOrder(root->right);
}void PostOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}PreOrder(root->left);PreOrder(root->right);
}int count = 0;
//不能定义局部变量count，因为每次函数的栈帧，增加的是自己的count
void TreeSize1(BTNode* root)
{if (root == NULL){return;}++count;TreeSize1(root->left);TreeSize1(root->right);
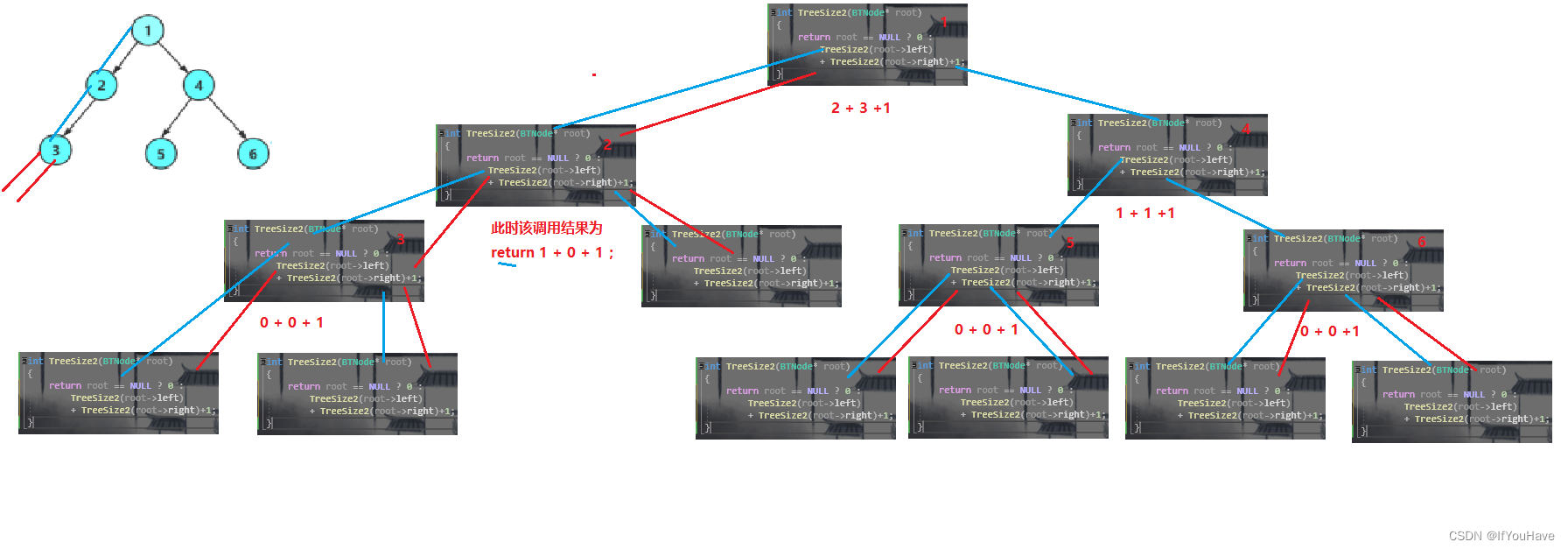
}int TreeSize2(BTNode* root)
{return root == NULL ? 0 : TreeSize2(root->left) + TreeSize2(root->right)+1;
}

#include"BinaryTree.h"
extern int count;
int main()
{BTNode* root = CreatBinaryTree();PreOrder(root);printf("\n");InOrder(root);printf("\n");PostOrder(root);printf("\n");//每次调用前将count结果置为空count = 0;TreeSize1(root);printf("%d\n",count);count = 0;TreeSize1(root);printf("%d\n", count);printf("%d\n", TreeSize2(root));printf("%d\n", TreeSize2(root));return 0;
}

TreeSize1 此时定义局部变量，在多线程调用，并行计数，就会失败

TreeSize2 此时运用分治思想，在任何情况，只要调用，便会返回size大小

分治思想

 求叶子节点数量，分治思想：

int TreeLeafSize(BTNode* root)
{if (root == 0){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

分治思想

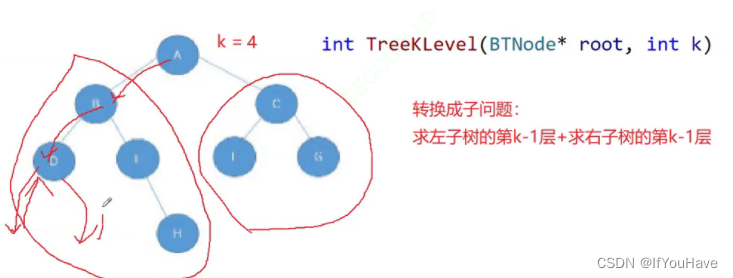
求第k层节点个数：

 

//求第k层节点个数
int TreeKLevel(BTNode* root, int k)
{assert(k >= 1);if (root == NULL){return 0;}if (k == 1);{return 1;}return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}

分治思想

求二叉树的深度：

//求二叉树的深度
int TreeDepth(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}int ret1 = TreeDepth(root->left) + 1;int ret2 = TreeDepth(root->right) + 1;return ret1 > ret2 ? ret1 : ret2;
}

分治思想

二叉树查找值为x的结点：

//二叉树查找值为x的结点
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* ret1 = TreeFind(root->left, x);if (ret1){return ret1;}BTNode* ret2 = TreeFind(root->right, x);if (ret2){return ret2;}return NULL;
}

5、二叉树基础oj练习

1. 单值二叉树。

965. 单值二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/univalued-binary-tree/

bool PreOrderCompare(struct TreeNode* root,int val)
{if(root == NULL){return true;}if(root->val != val){return false;}return PreOrderCompare(root->left,val) && PreOrderCompare(root->right,val);
}bool isUnivalTree(struct TreeNode* root){if(root == NULL){return true;}return PreOrderCompare(root,root->val);
}

bool isUnivalTree(struct TreeNode* root){if(root == NULL){return true;}if(root->left && root->left->val != root->val){return false;}if(root->right && root->right->val != root->val){return false;}return isUnivalTree(root->left) && isUnivalTree(root->right);//此时左边为false，右边就不进行运算，减少空间时间消耗
}

2、检查两颗树是否相同。

100. 相同的树 - 力扣（LeetCode）https://leetcode.cn/problems/same-tree/

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/bool isSameTree(struct TreeNode* p, struct TreeNode* q){if(p == NULL && q == NULL){return true;}if(p == NULL ||  q==NULL){return false;}if(p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right,q->right);}

3. 对称二叉树。

101. 对称二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/symmetric-tree/

 bool isSameTree(struct TreeNode* p, struct TreeNode* q){if(p == NULL && q == NULL){return true;}if(p == NULL ||  q==NULL){return false;}if(p->val != q->val){return false;}return isSameTree(p->left, q->right) && isSameTree(p->right,q->left);}
bool isSymmetric(struct TreeNode* root){if(root == NULL){return true;}return isSameTree(root->left,root->right);}

4. 二叉树的前序遍历。

144. 二叉树的前序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-preorder-traversal/submissions/

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/void preOrder(struct TreeNode* root,int* result,int* returnSize){if(root == NULL){return;}result[*returnSize] = root->val;(*returnSize) ++;preOrder(root->left,result,returnSize);preOrder(root->right,result,returnSize);}
int* preorderTraversal(struct TreeNode* root, int* returnSize){int* result = (int*)malloc(sizeof(int) * 1000);*returnSize = 0;preOrder(root,result,returnSize);return result;
}

5. 二叉树中序遍历 。

Loading Question... - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-inorder-traversal/

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*//*** Note: The returned array must be malloced, assume caller calls free().*/void inOrder(struct TreeNode* root,int* result,int* returnSize){if(root == NULL){return;}inOrder(root->left,result,returnSize);result[*returnSize] = root->val;(*returnSize) ++;inOrder(root->right,result,returnSize);}
int* inorderTraversal(struct TreeNode* root, int* returnSize){int* result = (int*)malloc(sizeof(int) * 1000);*returnSize = 0;inOrder(root,result,returnSize);return result;
}

6. 二叉树的后序遍历 。

145. 二叉树的后序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-postorder-traversal/

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*//*** Note: The returned array must be malloced, assume caller calls free().*/
void postOrder(struct TreeNode* root,int* result,int* returnSize){if(root == NULL){return;}postOrder(root->left,result,returnSize);postOrder(root->right,result,returnSize);result[*returnSize] = root->val;(*returnSize) ++;}
int* postorderTraversal(struct TreeNode* root, int* returnSize){int* result = (int*)malloc(sizeof(int) * 1000);*returnSize = 0;postOrder(root,result,returnSize);return result;
}

7. 另一颗树的子树。

力扣 (leetcode.cn)https://leetcode.cn/problems/subtree-of-another-tree/

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q){if(p == NULL && q == NULL){return true;}if(p == NULL ||  q==NULL){return false;}if(p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right,q->right);}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if(root==NULL){return false;}if(isSameTree(root,subRoot) == true){return true;}return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}