适用

bellman-ford算法适用于有负边，且最短路径有边数限制的题目。
如果没有边数的限制并且有负边我们一般用spfa算法。

讲解

其实和普通版的dijkstra差不多，略微有几处不同的地方。

• 1，我们每次能遍历到所有节点就行了，所以就用结构体存储就可以了，当然你用别的也是可以的。
• 2，在函数中第一次遍历，遍历多少次就代表最后有多少条边。限制变数的条件在这里实现。
• 3，这里有个last数组，就是备份上一次的，要不然更新的时候容易出现串联，就是因为每次要遍历所有的节点，每次要更新一条边，举个例子吧。
  
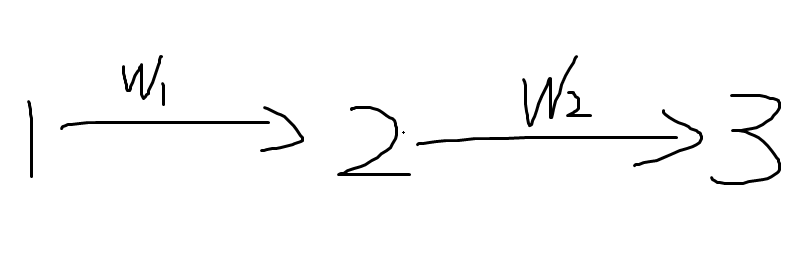
  假如说现在在j的for循环中，有一次更新了2的dist，但是我们我们在下一次更新3的时候我们不应该用2的w1权重，而是应该用2的上次的正无穷权重，因为一个i循环每个节点只能向外伸展一个节点。
• 4，然后就是普通的更新了，a到b有一条边，看a能不能把b更新了。
• 5，最后就是输出的时候，为什么要用dist[n] > 0x3f3f3f3f / 2呢，因为这是负权边，有可能倒数第二个节点到最后一个节点是个负权的，然后就把最后一个节点给更新了。图示…
  
• 6，因为函数中要用到m，所以输入的时候不能用while(m--)。

流程

来源AcWing

源码

#include using namespace std;const int N = 510, M = 10010;int n, m, k;
int dist[N];
int last[N];struct Edges
{int a, b, w;
}edges[M];void bellman_ford()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < k; i ++){memcpy(last, dist, sizeof dist);for (int j = 0; j < m; j ++ ){dist[edges[j].b] = min(dist[edges[j].b], dist[edges[j].a] + edges[j].w);}}	
}int main()
{cin >> n >> m >> k;for (int i = 0; i < m; i ++ ){int a, b, c;cin >> a >> b >> c;edges[i] = {a, b, c};}bellman_ford();if (dist[n] > 0x3f3f3f3f / 2) cout << "impossible" << "\n";else cout << dist[n] << "\n";
}