数据间的相似性度量

文章目录

• 数据间的相似性度量
• • 1. 欧氏距离的计算
  • • 1.1 一维数据间的欧氏距离
    • 1.2 多维数据间的欧氏距离
  • 2. 欧氏距离的矩阵表达
  • • 2. 代码实现
    • 2.2 调用机器学习库实现

常见的距离

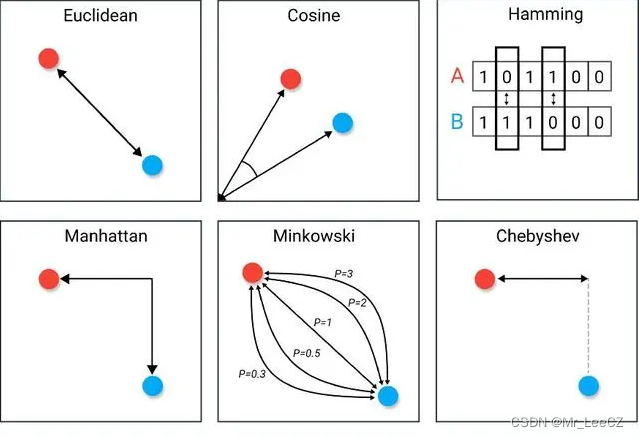
• 欧式距离:

d(x,y)=∑i=1n(xi−yi)2=∥x−y∥2d(\boldsymbol{x},\boldsymbol{y})=\sqrt{\sum_{i=1}^n(x_i-y_i)^2}=\Vert\boldsymbol{x}-\boldsymbol{y}\Vert_2 d(x,y)=i=1∑n​(xi​−yi​)2​=∥x−y∥2​

• cosine 距离

d(x,y)=x⊤⋅yd(\boldsymbol{x},\boldsymbol{y})=\boldsymbol{x}^\top\cdot\boldsymbol{y} d(x,y)=x⊤⋅y

• Mahattan 距离:

d(x,y)=∑i=1n∣xi−yi∣=∥x−y∥1d(\boldsymbol{x},\boldsymbol{y})=\sum_{i=1}^n\vert x_i-y_i\vert=\Vert\boldsymbol{x}-\boldsymbol{y}\Vert_1 d(x,y)=i=1∑n​∣xi​−yi​∣=∥x−y∥1​

• mikovski 距离

d(x,y)=∑i=1n∣xi−yi∣pp=∥x−y∥pd(\boldsymbol{x},\boldsymbol{y})=\sqrt[p]{\sum_{i=1}^n\vert x_i-y_i\vert^p}=\Vert\boldsymbol{x}-\boldsymbol{y}\Vert_p d(x,y)=pi=1∑n​∣xi​−yi​∣p​=∥x−y∥p​

1. 欧氏距离的计算

1.1 一维数据间的欧氏距离

def distance_1d(s):n = len(s)A = np.zeros((n,n))for i in range(n):for j in range(n):A[i,j] = abs(s[i]-s[j])return Aimport numpy as npif __name__ == "__main__":x = np.array([1,2,3,4,5])D = distance_1d(x)print(D)

1.2 多维数据间的欧氏距离

def distance_nd(S):nrow, ncol = S.shape # 获取输入矩阵的行数和列数A = np.zeros((nrow,nrow))for i in range(nrow):for j in range(nrow):summ = 0for k in range(ncol):summ = summ + (S[i,k]-S[j,k])**2A[i,j] = np.sqrt(summ)return Aimport numpy as npif __name__ == "__main__":X = np.random.randn(5,10)D = distance_nd(X)print(D)

2. 欧氏距离的矩阵表达

两个列向量(样本)之间的欧式距离表示为
d2(x,y)=∑k(xk−yk)2=(x−y)T(x−y)=x⊤x−2x⊤y+y⊤yd^2(\boldsymbol{x},\boldsymbol{y})=\sum_k(x_k-y_k)^2=(\boldsymbol{x}-\boldsymbol{y})^T(\boldsymbol{x}-\boldsymbol{y})=\boldsymbol{x}^\top\boldsymbol{x}-2\boldsymbol{x}^\top\boldsymbol{y}+\boldsymbol{y}^\top\boldsymbol{y} d2(x,y)=k∑​(xk​−yk​)2=(x−y)T(x−y)=x⊤x−2x⊤y+y⊤y

两个矩阵列与列之间的欧式距离表示为
d2(X,Y)=[x1⊤x1−2x1⊤y1+y1⊤y1x1⊤x1−2x1⊤y2+y2⊤y2⋯x1⊤x1−2x1⊤yN+yN⊤yNx2⊤x2−2x2⊤y1+y1⊤y1x2⊤x2−2x2⊤y2+y2⊤y2⋯x2⊤x2−2x2⊤yN+yN⊤yN⋮⋮⋱⋮xM⊤xM−2xM⊤y1+y1⊤y1xM⊤xM−2xM⊤y2+y2⊤y2⋯xM⊤xM−2xM⊤yN+yN⊤yN]=[x1⊤x1x1⊤x1⋯x1⊤x1x2⊤x2x2⊤x2⋯x2⊤x2⋮⋮⋱⋮xM⊤xMxM⊤xM⋯xM⊤xM]+[y1⊤y1y2⊤y2⋯yN⊤yNy1⊤y1y2⊤y2⋯y2⊤y2⋮⋮⋱⋮y1⊤y1y2⊤y2⋯yN⊤yN]−2[x1⊤y1x1⊤y2⋯x1⊤yNx2⊤y1x2⊤y2⋯x2⊤yN⋮⋮⋱⋮xM⊤y1xM⊤y2⋯xM⊤yN]=[x1⊤x1x2⊤x2⋮xM⊤xM]⋅[1,1,⋯,1]N+[11⋮1]M⋅[y1⊤y1,y2⊤y2,⋯,yN⊤yN]−2[x1⊤x2⊤⋮xM⊤]⋅[y1,y2,⋯,yN]\begin{array}{ll} d^2(X,Y)&= \left[\begin{array}{cccc} \boldsymbol{x}_1^\top\boldsymbol{x}_1-2\boldsymbol{x}_1^\top\boldsymbol{y}_1+\boldsymbol{y}_1^\top\boldsymbol{y}_1&\boldsymbol{x}_1^\top\boldsymbol{x}_1-2\boldsymbol{x}_1^\top\boldsymbol{y}_2+\boldsymbol{y}_2^\top\boldsymbol{y}_2&\cdots &\boldsymbol{x}_1^\top\boldsymbol{x}_1-2\boldsymbol{x}_1^\top\boldsymbol{y}_N+\boldsymbol{y}_N^\top\boldsymbol{y}_N\\ \boldsymbol{x}_2^\top\boldsymbol{x}_2-2\boldsymbol{x}_2^\top\boldsymbol{y}_1+\boldsymbol{y}_1^\top\boldsymbol{y}_1&\boldsymbol{x}_2^\top\boldsymbol{x}_2-2\boldsymbol{x}_2^\top\boldsymbol{y}_2+\boldsymbol{y}_2^\top\boldsymbol{y}_2&\cdots &\boldsymbol{x}_2^\top\boldsymbol{x}_2-2\boldsymbol{x}_2^\top\boldsymbol{y}_N+\boldsymbol{y}_N^\top\boldsymbol{y}_N\\ \vdots & \vdots & \ddots & \vdots&\\ \boldsymbol{x}_M^\top\boldsymbol{x}_M-2\boldsymbol{x}_M^\top\boldsymbol{y}_1+\boldsymbol{y}_1^\top\boldsymbol{y}_1&\boldsymbol{x}_M^\top\boldsymbol{x}_M-2\boldsymbol{x}_M^\top\boldsymbol{y}_2+\boldsymbol{y}_2^\top\boldsymbol{y}_2&\cdots& \boldsymbol{x}_M^\top\boldsymbol{x}_M-2\boldsymbol{x}_M^\top\boldsymbol{y}_N+\boldsymbol{y}_N^\top\boldsymbol{y}_N\\ \end{array} \right]\\\;\\ &=\left[\begin{array}{cccc} \boldsymbol{x}_1^\top\boldsymbol{x}_1&\boldsymbol{x}_1^\top\boldsymbol{x}_1&\cdots &\boldsymbol{x}_1^\top\boldsymbol{x}_1\\ \boldsymbol{x}_2^\top\boldsymbol{x}_2&\boldsymbol{x}_2^\top\boldsymbol{x}_2&\cdots &\boldsymbol{x}_2^\top\boldsymbol{x}_2\\ \vdots & \vdots & \ddots & \vdots&\\ \boldsymbol{x}_M^\top\boldsymbol{x}_M&\boldsymbol{x}_M^\top\boldsymbol{x}_M&\cdots& \boldsymbol{x}_M^\top\boldsymbol{x}_M\\ \end{array} \right]+ \left[\begin{array}{cccc} \boldsymbol{y}_1^\top\boldsymbol{y}_1&\boldsymbol{y}_2^\top\boldsymbol{y}_2&\cdots &\boldsymbol{y}_N^\top\boldsymbol{y}_N\\ \boldsymbol{y}_1^\top\boldsymbol{y}_1&\boldsymbol{y}_2^\top\boldsymbol{y}_2&\cdots &\boldsymbol{y}_2^\top\boldsymbol{y}_2\\ \vdots & \vdots & \ddots & \vdots&\\ \boldsymbol{y}_1^\top\boldsymbol{y}_1&\boldsymbol{y}_2^\top\boldsymbol{y}_2&\cdots& \boldsymbol{y}_N^\top\boldsymbol{y}_N\\ \end{array} \right]\\\;\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad-2\left[\begin{array}{cccc} \boldsymbol{x}_1^\top\boldsymbol{y}_1&\boldsymbol{x}_1^\top\boldsymbol{y}_2&\cdots &\boldsymbol{x}_1^\top\boldsymbol{y}_N\\ \boldsymbol{x}_2^\top\boldsymbol{y}_1&\boldsymbol{x}_2^\top\boldsymbol{y}_2&\cdots &\boldsymbol{x}_2^\top\boldsymbol{y}_N\\ \vdots & \vdots & \ddots & \vdots&\\ \boldsymbol{x}_M^\top\boldsymbol{y}_1&\boldsymbol{x}_M^\top\boldsymbol{y}_2&\cdots& \boldsymbol{x}_M^\top\boldsymbol{y}_N\\ \end{array} \right]\\\;\\ &=\left[\begin{array}{c} \boldsymbol{x}_1^\top\boldsymbol{x}_1\\ \boldsymbol{x}_2^\top\boldsymbol{x}_2\\ \vdots\\ \boldsymbol{x}_M^\top\boldsymbol{x}_M \end{array}\right]\cdot[1,1,\cdots,1]_N +\left[\begin{array}{c} 1\\ 1\\ \vdots\\ 1 \end{array}\right]_M\cdot[\boldsymbol{y}_1^\top\boldsymbol{y}_1,\boldsymbol{y}_2^\top\boldsymbol{y}_2,\cdots,\boldsymbol{y}_N^\top\boldsymbol{y}_N] -2\left[\begin{array}{c} \boldsymbol{x}_1^\top\\ \boldsymbol{x}_2^\top\\ \vdots\\ \boldsymbol{x}_M^\top \end{array}\right]\cdot[\boldsymbol{y}_1,\boldsymbol{y}_2,\cdots,\boldsymbol{y}_N] \end{array} d2(X,Y)​=​x1⊤​x1​−2x1⊤​y1​+y1⊤​y1​x2⊤​x2​−2x2⊤​y1​+y1⊤​y1​⋮xM⊤​xM​−2xM⊤​y1​+y1⊤​y1​​x1⊤​x1​−2x1⊤​y2​+y2⊤​y2​x2⊤​x2​−2x2⊤​y2​+y2⊤​y2​⋮xM⊤​xM​−2xM⊤​y2​+y2⊤​y2​​⋯⋯⋱⋯​x1⊤​x1​−2x1⊤​yN​+yN⊤​yN​x2⊤​x2​−2x2⊤​yN​+yN⊤​yN​⋮xM⊤​xM​−2xM⊤​yN​+yN⊤​yN​​​​=​x1⊤​x1​x2⊤​x2​⋮xM⊤​xM​​x1⊤​x1​x2⊤​x2​⋮xM⊤​xM​​⋯⋯⋱⋯​x1⊤​x1​x2⊤​x2​⋮xM⊤​xM​​​​+​y1⊤​y1​y1⊤​y1​⋮y1⊤​y1​​y2⊤​y2​y2⊤​y2​⋮y2⊤​y2​​⋯⋯⋱⋯​yN⊤​yN​y2⊤​y2​⋮yN⊤​yN​​​​−2​x1⊤​y1​x2⊤​y1​⋮xM⊤​y1​​x1⊤​y2​x2⊤​y2​⋮xM⊤​y2​​⋯⋯⋱⋯​x1⊤​yN​x2⊤​yN​⋮xM⊤​yN​​​​=​x1⊤​x1​x2⊤​x2​⋮xM⊤​xM​​​⋅[1,1,⋯,1]N​+​11⋮1​​M​⋅[y1⊤​y1​,y2⊤​y2​,⋯,yN⊤​yN​]−2​x1⊤​x2⊤​⋮xM⊤​​​⋅[y1​,y2​,⋯,yN​]​

若对数据矩阵本身求两两(列表示样本点)之间的欧式距离,则计算表达式可简单表示为

d2(X,X)=diag(X⊤X)⋅1⊤+1⋅diag(X⊤X)−2X⊤Xd^2(X,X)=\text{diag}(X^\top X)\cdot\boldsymbol{1}^\top+\boldsymbol{1}\cdot\text{diag}(X^\top X)-2X^\top X d2(X,X)=diag(X⊤X)⋅1⊤+1⋅diag(X⊤X)−2X⊤X

2. 代码实现

import numpy as npX = np.array([[1,2,3,4,5,6,7,8,9],[1,1,1,1,1,1,1,1,1]])
D, N = X.shape
print('LLE running on {} points in {} dimensions\n'.format(N,D))G = X.T@X
H = np.diag(G).reshape(-1,1)@np.ones((1,9))
dist = H+H.T-2*G
dist = np.sqrt(dist)
print(dist)
print('\n')
index = np.argsort(dist,axis=0)
neighborhood = index[1:5,:] 
print(neighborhood)

2.2 调用机器学习库实现

import numpy as np
from sklearn.metrics.pairwise import paired_distancesX = np.array([[1,2,3,4,5,6,7,8,9],[1,1,1,1,1,1,1,1,1]])
dist = paired_distances(X,X)
print(dist)
print('\n')
index = np.argsort(distance,axis=0)
print(index)
print('\n')
neighborhood = index[1:5,:] 
print(neighborhood)