文章目录

• 一、排序相关概念
• • 1, 什么是排序
  • 2, 什么是排序的稳定性
  • 3, 七大排序分类
• 二、选择排序
• • 1, 图文解析
  • 2, 代码实现
• 三、性能分析
• 四、七大排序算法总体分析

提示：是正在努力进步的小菜鸟一只，如有大佬发现文章欠佳之处欢迎评论区指点~ 废话不多说，直接发车~

一、排序相关概念

1, 什么是排序

📌排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增📈或递减📉的排列起来的操作

👉以 int 类型数据从小到大排序为例：
排序前：4，1，3，6，8，7，2，5
排序后：1，2，3，4，5，6，7，8

2, 什么是排序的稳定性

📌稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

👉以 int 类型数据从小到大排序为例：
排序前：4，1，3a，6，8，7，2，3b，5（3a 在 3b 之前）
排序后：1，2，3a，3b，4，5，6，7，8（3a 还在 3b 之前，稳定）
排序后：1，2，3b，3a，4，5，6，7，8（3a 不在 3b 之前，不稳定）

3, 七大排序分类

以下是常见的 7大排序 算法

二、选择排序

1, 图文解析

📌选择排序 就是通过 n-i次比较,从n-i+1个数据中找到最小的一个记录, 并且和第 i 个数据交换

📌算法思想: 每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完 。

比如你预算充足的情况的下, 想选择一辆座驾🚗
1️⃣一开始在网上看上了一台 50w 奔驰E, 觉得蛮不错,这是你的第一个目标座驾
2️⃣然后你到了 4s 店, 往里走看到了 120w 的奔驰S比奔驰E的内饰更漂亮舒适, 外观更霸气, 于是又想买奔驰S
3️⃣接着再往里走看到了 180w 的奔驰AMGE63, 觉得这要性能有性能,要外观有外观, 于是又想买奔驰AMGE63
4️⃣最后等到去交钱签合同的时候,看到了奔驰最尊贵的座驾----- 500w 的迈巴赫更符合你尊贵的身份, 于是当机立断选择了迈巴赫

50w 是一个标准,然后找到了 120w , 暂时选择了1 20w ----后来又找到了 180w , 暂时选择了 180w ----最后又找到了 500w 的迈巴赫, 这已经是最贵的得了, 所以最终选择了 500w 的代替了 50w 的

这就是选则排序的思想

我们反过来,给定你一组数据
1️⃣第一个数据是300,暂时作为标准,
2️⃣在数组中往后找,找到了180,把180记录为最小值
3️⃣又找到了120,把120作为最小值
4️⃣又找到了50,把50最为最小值
没有比50更小的了,让最小值50和300 交换 , 值最小的50来到了前面,而相对比较大的300来到了后面

那么给定一组无序的数据, 实现直接插入排序的具体过程是什么呢? 如图所示
注意 i , j 下标的变化

❗️❗️注意,这里只分析了一躺排序,并没有把整个数组排有序

理解了过程,来看一下代码如何实现

2, 代码实现

  /*** 选择排序* 时间复杂度：O(N^2)* 空间复杂度：O(1)* 稳定性：不稳定* @param array*/public static void selectSort(int[] array) {if(array == null) {return;}for (int i = 0; i < array.length; i++) {int minInedx = i;int j = i + 1;for (; j < array.length; j++) {if (array[j] < array[minInedx]) {minInedx = j;}}swap(array, minInedx, i);}}

七大排序算法中会经常使用到交换, 所以单独封装一个方法出来

    private static void swap(int[] array,int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}

三、性能分析

👉时间复杂度:
最好最差情况,选择排序的数据之间的比较次数都是固定的,
而最好情况:数组有序时,需要交换0次,最坏情况:数组无序时,交换n-1次
总体的排序时间是比较+交换的总和,所以时间复杂度为O(N^2)

选择排序理解和实现起来都比较简单,但效率比较低,一般很少使用选择排序

👉空间复杂度:
没有额外空间的开销,只有常数个记录的辅助空间,空间复杂度为O(1)

👉稳定性:
不稳定

四、七大排序算法总体分析

建议对七大算法都有认识之后, 再对比分析~~

没有完美的排序算法,任何一种算法都是有优点和缺陷的,即便是大名鼎鼎的快速排序,也只是整体上效率比较高,性能相对更优越

现在就整体分析一下各种排序的优缺点📊

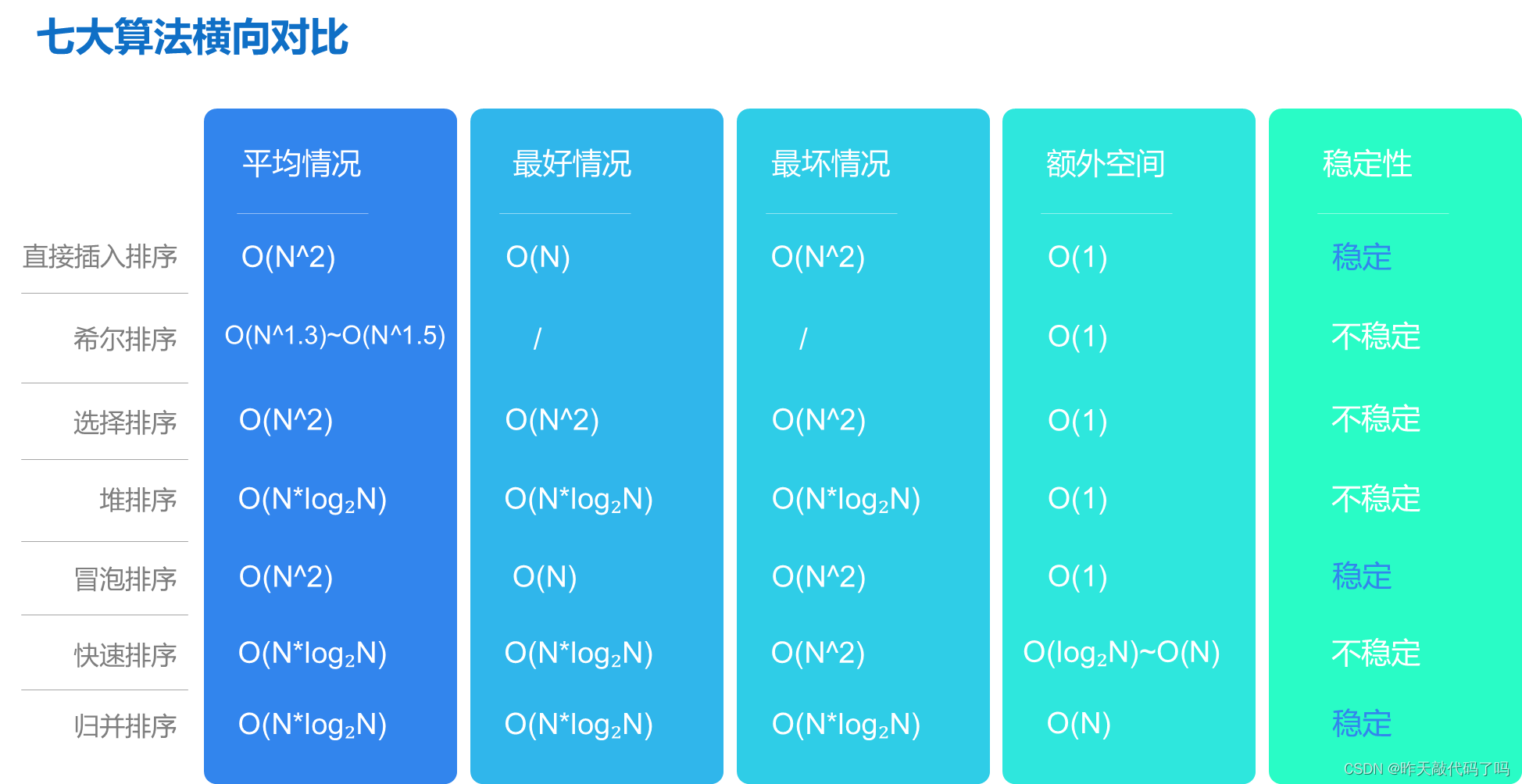
早期的排序算法平均时间复杂度都是O(N^2); 因为原理比较简单, 但性能较差, 所以 一般把直接插入排序,选择排序,冒泡排序归为简单排序一类 其他的都归于 改进排序

📚从平均情况看:
改进过的排序: 希尔排序, 堆排序, 归并排序, 快速排序要胜过 简单排序的性能, 而四个改进算法中, 希尔排序的性能最差

📚从最好情况看:
直接插入排序和冒泡排序最快

📚从最坏情况看:
堆排序和归并排序的性能更胜过快排和其他简单排序

📚综合来看:
堆排序和归并排序比较稳定和强大, 情况最坏时好使
直接插入排序和冒泡排序在基本有序时最好用,
而快速排序比较极端, 最好最坏情况都有缺陷 但是 快速排序能够称之为快速排序, 是因为它的综合性能最强💪，一般情况下是最快的

📚从稳定性来看:
改进排序中只有归并排序

📚从数据个数上看:
数据量越少, 越适合用简单排序, 因为堆排, 快速排序, 归并排序, 都用到了递归, 对于少量数据排序有点"炮弹打蚊子"

只要是交换时, 两数据相邻就是稳定的算法,只要是跳跃式的交换就是不稳定, 当然别忘了, 稳定的算法也可以修改代码更改成不稳定的

如果本篇对你有帮助，请点赞收藏支持一下，小手一抖就是对作者莫大的鼓励啦😋😋😋~

上山总比下山辛苦
下篇文章见