题目描述：

小明有一个大小为N×M的矩阵，可以理解为一个N行M列的二维数组。 我们定义一个矩阵m 的稳定度f(m)
为f(m)=max(m)-min(m)。 其中max(m)表示矩阵m中的最大值，min(m) 表示矩阵m 中的最小值。
现在小明想要从这个矩阵中找到一个稳定度不大于limit 的子矩阵； 同时他还希望这个子矩阵的面积越大越好（面积可以理解为矩阵中元素个数）。

子矩阵定义如下：

从原矩阵中选择一组连续的行和一组连续的列，这些行列交点上的元素组成的矩阵即为一个子矩阵。

输入格式：

第一行输入两个整数N，M，表示矩阵的大小。 接下来N 行，每行输入M 个整数，表示这个矩阵。 最后一行输入一个整数limit，表示限制。

对于所有评测用例，0≤矩阵元素值, limit≤10^5。

输出格式：

输出一个整数，分别表示小明选择的子矩阵的最大面积。

输入样例：

3 4
2 0 7 9
0 6 9 7
8 4 6 4
8

输出样例：

6

数据范围与提示

满足稳定度不大于8 的且面积最大的子矩阵总共有三个，他们的面积都是6（粗体表示子矩阵元素）：

2 0 7 9
0 6 9 7
8 4 6 4

2 0 7 9
0 6 9 7
8 4 6 4

2 0 7 9
0 6 9 7
8 4 6 4

解题思路：

本题采用dfs + 回溯的思想来解决，也就是朴素的暴搜。

若要利用好深搜索得先搞清以下问题：

1.应先明确遍历的起点：
数组中每个元素都可以是起点，这样能无死角地找到所有符合条件的子矩阵。 所以我们要对数组内每个点都进行遍历，不断更新面积最大值。

2.如何知道我们遍历过的符合条件的区域是一个矩阵？（这是我们更新子矩阵面积所必需要知道的。）

“对号”部分是是我们遍历过的区域。

很明显这不是一个矩阵，但是若我们知道遍历过的点的横坐标范围，和纵坐标的范围，问题就解决了。

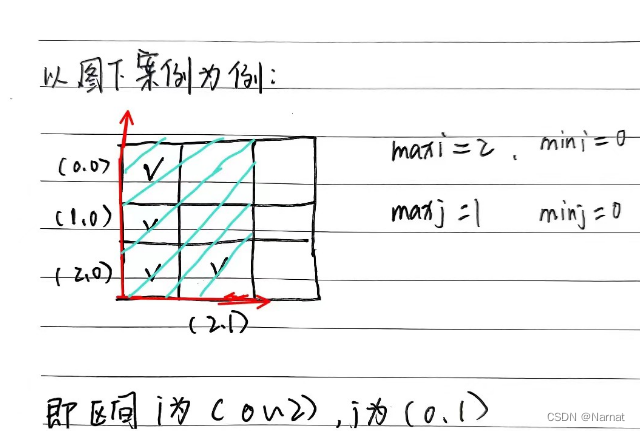
知道范围后，在这个范围内（即蓝色区域内）遍历一下看看是不是所有点都被遍历过，是则满足子矩阵，否则不满足，这需要单独构建一个布尔数组，和一个判断是否为矩阵的函数。

3.遍历规则：
我们知道 深度优先遍历是一个路径，而我们想要的是子矩阵。
即如果我么们给的限制条件只是在数组区间内遍历，那么它就会在这个区间乱窜。所以我么们需要施加新条件来限制它的遍历轨迹，确保以遍历子矩阵为优先。
即，如果当前遍历路径不是子矩阵的话，我们就将当前所在矩阵区域遍历满。如果当前遍历区域是一个子矩阵的话，我们就扩大边界，试着去得到面积更大的符合条件的子矩阵。

4.遍历过程的模拟：

理清思路后我们可以模拟一下遍历过程，以确保万无一失。想学好 dfs 会模拟自己写的程序是必不可少的。

以题目中例1的遍历为例以下是我的模拟过程，可以助于理解：

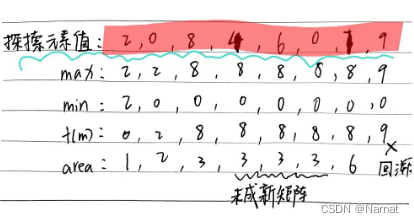
理论成立代码如下：

import java.util.Scanner;public class Main {public static int n = 0;public static int m = 0;public static void main(String[] args){Scanner sc = new Scanner(System.in);n = sc.nextInt();m = sc.nextInt();int a[][] = new int[n + 10][m + 10];//储存数组visit = new boolean[n][m];for(int i = 0; i < n; i ++)for(int j = 0; j < m; j ++) a[i][j] = sc.nextInt();f = sc.nextInt();for(int i = 0; i < n; i ++)for(int j = 0; j < m; j ++) {mini = i;minj = j;maxi = i;maxj = j; sunmatrix = 1;minvalue = a[i][j];maxvalue = a[i][j];	   // 初始化visit[i][j] = true;//标记dfs(a, i, j);visit[i][j] = false;//回溯maxsmatrix = Math.max(sunmatrix, maxsmatrix);//更新}System.out.print(maxsmatrix);//最终结果}public static boolean visit[][];//储存路径public static int mini = 0;public static int maxi = 0;public static int minj = 0;public static int maxj = 0;//储存矩阵范围public static int f = 0;//储存题目要求稳定度public static int minvalue = 0;public static int maxvalue = 0;//储存遍历过的路径最大值与最小值public static int sunmatrix = 0;//储存每次遍历最大面积public static int maxsmatrix = 0; // 储存最终答案public static void updatemx(int i, int j) {//更新遍历的矩阵范围mini = Math.min(mini, i);minj = Math.min(minj, j);maxi = Math.max(maxi, i);maxj = Math.max(maxj, j);}public static int F(int value) {//判断矩阵稳定度minvalue = Math.min(minvalue, value);maxvalue = Math.max(maxvalue, value);//更新return maxvalue - minvalue;}public static void dfs(int a[][], int i, int j) {int bfminvalue = minvalue;int bfmaxvalue = maxvalue;if(ifmatrix() && F(a[i][j]) <= f)//最重要的事情最先做，如果路径满足矩阵且新点符合条件，更新子矩阵面积sunmatrix = Math.max(sunmatrix, (maxi - mini + 1) * (maxj - minj + 1));//新子矩阵面积计算过程minvalue = bfminvalue;maxvalue = bfmaxvalue;//回溯int fxx = 0, fyy = 0;int fx[] = {-1, 1, 0, 0};int fy[] = {0, 0, -1, 1};//上下左右for(int k = 0; k < 4; k ++) {fxx = i + fx[k];fyy = j + fy[k];int bfmini = mini;int bfmaxi = maxi;int bfminj = minj;int bfmaxj = maxj; bfminvalue = minvalue;bfmaxvalue = maxvalue;//存着用于回溯if(ifmatrix()) {//是矩阵，扩张if(fxx >= 0 && fxx < n && fyy >= 0 && fyy < m && visit[fxx][fyy] != true && F(a[fxx][fyy]) <= f) {visit[fxx][fyy] = true;//标记来过updatemx(fxx, fyy);//更新边界dfs(a, fxx, fyy);visit[fxx][fyy] = false;}}else {//否者把目前范围矩阵遍历完if(fxx >= mini && fxx <= maxi && fyy >= minj && fyy <= maxj && visit[fxx][fyy] != true && F(a[fxx][fyy]) <= f) {visit[fxx][fyy] = true;updatemx(fxx, fyy);dfs(a, fxx, fyy);visit[fxx][fyy] = false;}}minvalue = bfminvalue;maxvalue = bfmaxvalue;//回溯mini = bfmini;minj = bfminj;maxi = bfmaxi;maxj = bfmaxj;}}public static boolean ifmatrix() {//判断此路径是否是矩阵for(int i = mini; i <= maxi; i ++)for(int j = minj; j <= maxj; j ++)if(visit[i][j] != true)  return false;return true;}}

此代码虽然长，但只要弄懂上述问题，逐一解决，条理还是很清晰的，本代码在官方平台上测试能搞到九成分数，剩下的两个测试点是超时了。能对的都对了。想拿满分的话可以看看别的大佬写的别的方法，对于我来说如果真让我在赛场上遇到这道题的话，我能用这个朴素爆搜混点分就很满足的，打死也想不出其他方法了。

此代码能优化的我也优化了，如果有些地方还可以优化的话，欢迎各大佬指点。