[LeetCode周赛复盘] 第 326 场周赛20230101
创始人
2024-05-30 22:17:34
[LeetCode周赛复盘] 第 326 场周赛20230101
- 一、本周周赛总结
- 二、 [Easy] 2582. 递枕头
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 三、[Medium] 2583. 二叉树中的第 K 大层和
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 四、[Medium] 2584. 分割数组使乘积互质
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 五、[Hard] 2585. 获得分数的方法数
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
一、本周周赛总结
- T1 模拟/数学。
- T2 二叉数层序遍历。
- T3 分解质因数。
- T4 分组背包。
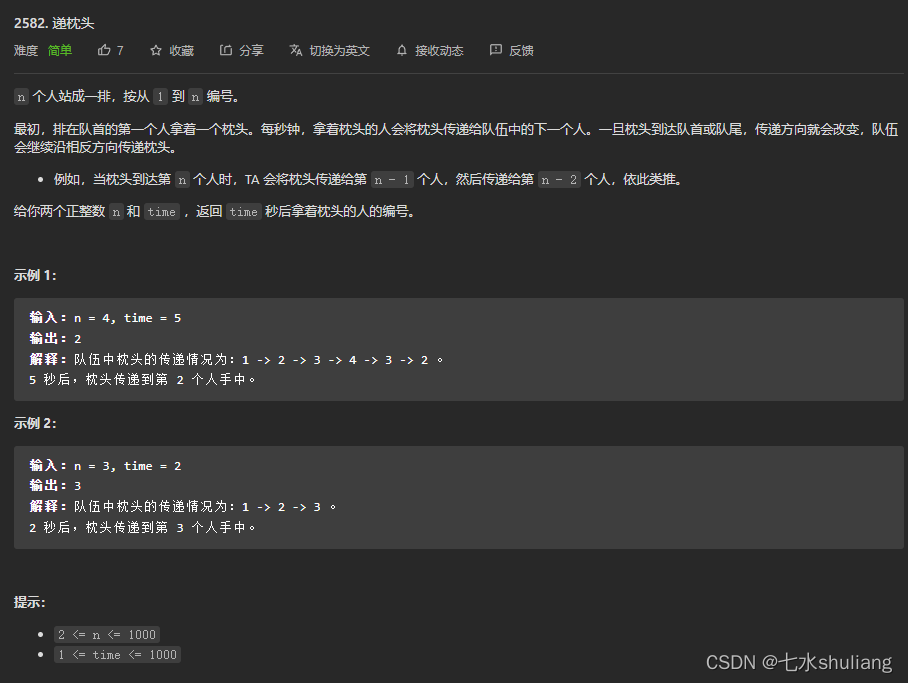
二、 [Easy] 2582. 递枕头
链接: 2582. 递枕头
1. 题目描述
2. 思路分析
按题意模拟即可。
3. 代码实现
class Solution:def passThePillow(self, n: int, time: int) -> int:ans = 1d = 1for _ in range(time):ans += dif ans > n:ans = n-1d *= -1elif ans < 1:ans = 2d *= -1return ans
三、[Medium] 2583. 二叉树中的第 K 大层和
链接: 2583. 二叉树中的第 K 大层和
1. 题目描述

2. 思路分析
- 层序遍历即可。
3. 代码实现
class Solution:def kthLargestLevelSum(self, root: Optional[TreeNode], k: int) -> int:a =[]q = deque([root])while q:s = 0for o in q:s += o.val a.append(s)for _ in range(len(q)):o = q.popleft()if o.left:q.append(o.left)if o.right:q.append(o.right)if len(a)四、[Medium] 2584. 分割数组使乘积互质
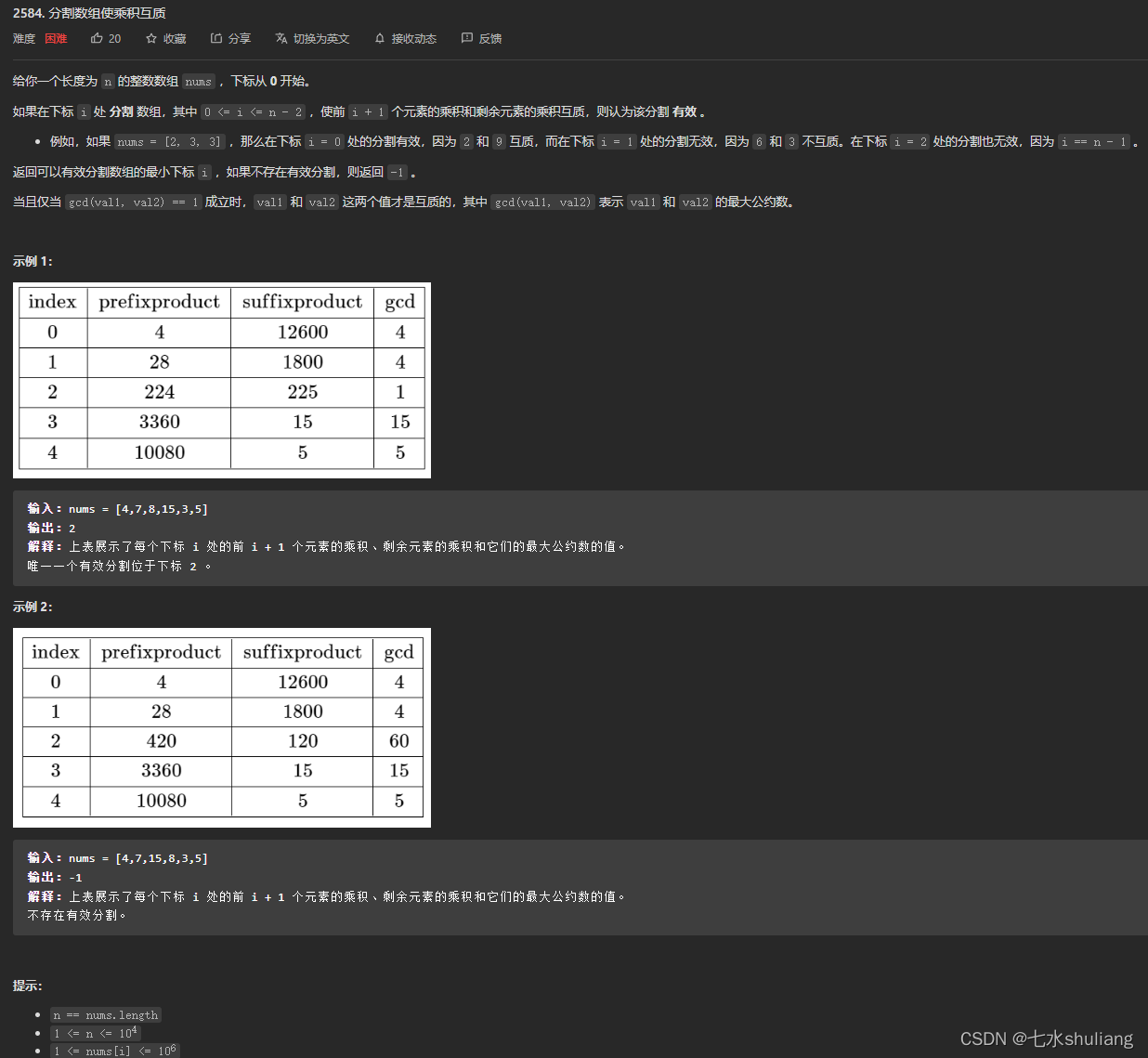
链接: 2584. 分割数组使乘积互质
1. 题目描述
2. 思路分析
- 分解质因数计数。
- 对整个数组分解质因数计数。判断前后缀里的质因数不相交即可。
- 实现时遍历前缀质因数计数,判断这里的所有质因数数量都等于总数里的数量。
3. 代码实现
def tag_primes_eratosthenes(n): # 返回一个长度n的数组p,如果i是质数则p[i]=1否则p[i]=0primes = [1]*nprimes[0] = primes[1] = 0 # 0和1不是质数for i in range(2,int(n**0.5)+1):if primes[i]:primes[i * i::i] = [0] * ((n - 1 - i * i) // i + 1)return primes
primes = tag_primes_eratosthenes(10**6+5)@cache
def get_prime_reasons(x):if x == 1:return Counter()if primes[x]:return Counter([x])for i in range(2,int(x**0.5)+1):if x % i == 0:return get_prime_reasons(i) + get_prime_reasons(x//i) class Solution:def findValidSplit(self, nums: List[int]) -> int:n = len(nums)cnt = Counter() # 整个数组所有质因子计数for v in nums:cnt += get_prime_reasons(v)p = Counter() # 前缀质因子计数diff = 0 # 前缀中质因子和整体不同的数量for i,v in enumerate(nums):c = get_prime_reasons(v)for k,cc in c.items():if k not in p:diff += 1p[k] += ccif p[k] == cnt[k]:diff -= 1# 若前缀中所有质因子都和整体相同,则前后缀一定没有交集if diff == 0 and i < n-1: # 注意这里一定要写在枚举数字之后而不是diff-=1之后,如果答案是0,如[1,1]会被hack掉。这是因为数字有可能没有质因数,不会进行diff的加减。return ireturn -1
五、[Hard] 2585. 获得分数的方法数
链接: 2585. 获得分数的方法数
1. 题目描述

2. 思路分析
- 这题是分组背包而不是多重背包,可以认为每种商品是一组,组里有count种商品,体积分别是分别是marks1、marks2…marks*count
3. 代码实现
MOD = 10**9+7class GroupedPackCountPlan:""" 分组背包问题求方案数,复杂度O(体积*物品(种类)数),一般求方案数很大,都要取模,这里为了防止忘记取模/模写错,直接调用全局变量,如果忘记定义会报错。注意和求极值不同:1. dp[0][0] = 1代表 一个不取的方案数是12. 数组里只需要一列体积参数,不需要价值。一般是01背包,完全背包。可能无法处理多重背包,因为无法区分同种类物品。这时尝试考虑分组背包,把每种物品看成一组,这组里的物品分别是1个i,2个i..c个i。"""def __init__(self, vol, grouped_items=None):self.grouped_items = grouped_items # 用于01背包的物品 (v):体积 self.vol = vol # 背包容量,注意计算复杂度时要用到self.f = [1] + [0] * vol # f[j]代表体积j时的方案,如果是求min这里初始值要改成infdef grouped_pack(self, items): # 注意传进来的是本组的物品的体积们:[1,6,2,3,4,5..],最好是排序的可以优化一下breakf = self.ffor j in range(self.vol, 0, -1): # 注意外层循环遍历体积j,内层尝试放组内每个物品。for v in items:if j >= v: # 这里可以尝试sort break,但是最好能在外层预处理或者天然是排序的。f[j] = (f[j]+f[j - v] )%MOD def run(self):"""直接计算这些背包的转移,除了很模板的题不建议使用"""if self.grouped_items:for v in self.grouped_items:self.grouped_pack(items) return self.fclass Solution:def waysToReachTarget(self, target: int, types: List[List[int]]) -> int: gp = GroupedPackCountPlan(target)for count,marks in types:items = [] # 本组物品的体积相当于尝试用k个marks,其中k<=countfor i in range(1,count+1):items.append(marks*i)gp.grouped_pack(items) # 整理好本组物品再一起传进去 return gp.f[-1] % MOD
六、参考链接
相关内容
热门资讯
最新或2023(历届)贺州产假...
省份 婚假 晚婚假 产假 陪产假(护理假) 广西 3天 原12天取消 148天 25天 上表中的1...
最新或2023(历届)百色产假...
省份 婚假 晚婚假 产假 陪产假(护理假) 广西 3天 原12天取消 148天 25天 上表中的1...
最新或2023(历届)玉林产假...
省份 婚假 晚婚假 产假 陪产假(护理假) 广西 3天 原12天取消 148天 25天 上表中的1...
最新或2023(历届)贵港产假...
省份 婚假 晚婚假 产假 陪产假(护理假) 广西 3天 原12天取消 148天 25天 上表中的1...
最新或2023(历届)钦州产假...
省份 婚假 晚婚假 产假 陪产假(护理假) 广西 3天 原12天取消 148天 25天 上表中的1...
