【C++】树?堆?怎么实现?
新的一周过去了,大家有没有对上星期练习的题目更加熟练呢?
上星期和上上星期我们主要学习了顺序表,链表,和用这俩都能实现的栈和队列
那么今天我们看看堆又是什么结构
目录
1.树 介绍
2.堆 介绍
3.堆的实现
1.树の介绍

不就是树,谁没见过对吧
那么类似的计算机也有一种树,很像我们学过的树状图

为了规范使用,先定义一些名称

层数和高度如你所见 就是你理解的意思
其实我们发现,这个命名规则就很像遗传族谱,其中也是借用了遗传族谱的一些名称
我们可以类比理解一下兄弟节点,堂兄弟节点,父子节点。。。
节点的祖先,是指从该节点网上走的唯一路径上经历的所有节点都是他的 节点的祖先
我们规定:树和树之间不能交叉!!!
森林:互不相交的树构成的结构~~
这只是最普通的树,还有一些稍微长得特殊一点的树
二叉树:每个父节点都有两个枝丫
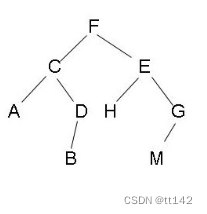
二叉树里面又有两种
满二叉树:每一层都是满的节点
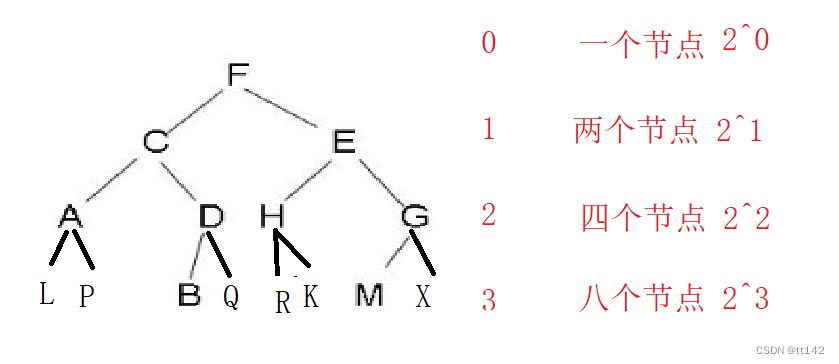
根据等比公式,满二叉树的高度为h(本图是4)那么节点个数就是2^h-1
第k层是满的,那么那一层的节点个数是2^(k-1) ,k从1开始
完全二叉树:最后一层可以不满,但是前面层数必须满,必须从左到右连续

大家自己去算一下,和刚才的方法一样的
完全二叉树的高度是h,那么总结点最多2^h-1 最少2^(h-1)
还有一些小小的二叉树计算技巧~
1.度为0的节点个数比度为2的节点个数多1
2.完全二叉树度为1 的节点个数不是0就是1
3.要计算叶子节点个数的题目,就是s算度为0,可以假设度为0有N0个,度为1有N1,度为2有N2
再根据 前两个技巧建立方程就好了
简单的基础知识就是这么多,那么真的在内存中就是有一块空间存储这些小圈和直线吗?
当然不是!!!!!!
这个树形状的图只是帮助我们人理解的(人家计算机根本不用借助图好吧)
所以这个图就是一种假想的模型,术语叫做 逻辑结构!!!(逻辑不好得用他帮助理解)
那么就该思考了,真实的内存结构(术语:物理结构)是什么样子
对于堆 其实是数组~
更复杂的现在不讨论
那么对于一般的树,他的“遗传图谱”怎么表示出来啊~~~
有个大神,想到了一种很![]() 的方法
的方法
struct TreeNode
{
int data;
TreeNode* child;
TreeNode* brother;
};我们细想一下,如果从最开始的根,我知道他的 孩子节点 和 孩子节点的兄弟节点
那简直就是完美解决整个图谱

直呼大佬![]()
2.堆的介绍
大家肯定在C的时候就对堆耳熟能详,现在我们主要看一下更深层次的理解
刚才说过,对
他的存放方式是这样的

从0开始编号,是为了和数组从0开始很好的对应
我们可以心里想着左图 但是不能不清楚他的真实结构是右图!!!
一个随随便便的数组不一定是堆,但是堆一定是一个数组
给你一个数组怎么判断他到底是不是一个堆?
首先我们要清楚堆的分类
大堆:每一个父节点都比他的子节点大

小堆:每一个父节点都比他的子节点小

所以我们只要看是不是大/小堆其中一种就行
比如数组{1,4,5,8,99} 1比4 5都小,4比8和99都小,所以这就是一个小堆,即堆
从中可以看出,对于数组你能不能一眼看出谁是谁的孩子,是左孩子还是右孩子?很重要
因为堆是完全二叉树 ,所以每个节点最多肯定是2个孩子
第一个数据1一定是根,往下两个4 5就是根(1)的孩子节点,在前面的4是左孩子
8,99是4,5中靠前数据(即4)的孩子节点,同样的8是左孩子
对应上我们刚才学的父子节点,不能拿发现父子节点的下标其实有规律
左孩子下标=父亲下标*2+1 因为左孩子的下标总是奇数!!
右孩子下标=父亲下标*2+2 因为左孩子的下标总是偶数!!
父亲下标=(孩子(左/右)-1)/2
3. 堆的实现(重点重点)
既然我们这么了解堆的结构,那么上手吧
这个实现和顺序表就很相似了
还是定义一个结构体,也就是表示一个节点
a表示结构体指针,可以用指针的方式访问数组
size是数组中元素的个数
capacity是容量,当容量和元素个数相等的时候要考虑扩容(老生常谈了)
把数据类型重定义可以方便以后存放不同类型的数据
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}Heap;//打印
void HeapPrint(Heap* hp);
//交换
void Swap(HPDataType* a, HPDataType* b);
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
//向上调整
void AdjustUp(HPDataType* a, int chirld);
//向下调整
AdjustDown(HPDataType* a, int n, int parent);
//初始化
void HeapInit(Heap* hp);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
void PrintTopK(int* a, int n, int k);主要的几个功能就是(按我的代码顺序)
打印(为了方便调试看结果的没什么含金量,大家自己就能完成)
//打印
void HeapPrint(Heap* hp)
{assert(hp);for (int i=0;isize;i++){printf("%d ", hp->a[i]);}printf("\n");
}
堆的初始化(指针a开不开空间都可以)
//初始化
void HeapInit(Heap* hp)
{assert(hp);hp->a = NULL;hp->capacity = hp->size = 0;
}
堆的构建:给你一个杂乱的数组,把他变成堆的形式(以大堆为例)
首先肯定是把所给数组中的数据都拷贝到结构体变量hp的指针a指向的数组里面啊
由于我们在初始化指针a的时候是没有开空间的(开不开都行,我写的是没开的版本,开了的话要先考虑扩容问题)
想到memcpy

拷贝好之后就要考虑是不是符合我大堆的定义
也就是考虑
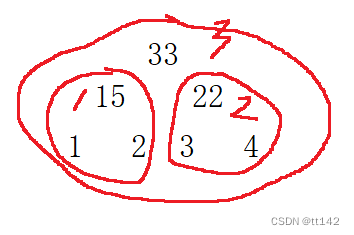
这三个子树是不是符合父节点比子节点大的要求,可以向下调整的方法,把父节点下标传给一个向下调整的函数作为家长节点下标,把容量和指针他也传过去
向下调整函数
AdjustDown(HPDataType* a, int n, int parent)
{assert(a);int child = 2 * parent + 1;//假设是左孩子,并且左孩子是最大的孩子while (child a[child] && child+1 其中还复用了一个交换值的函数,由于后面交换的地方较多,最好还是交给函数去做
//交换
void Swap(HPDataType* a, HPDataType* b)
{HPDataType tmp = *a;*a = *b;*b = tmp;
}
我们发现我标记的1 2 3其实是连续的下标!!
所以堆创建函数
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{assert(hp);hp->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (hp->a == NULL){perror("HeapCreate fail");exit(-1);}memcpy(hp->a, a, n*sizeof(HPDataType));hp->size = hp->capacity=n;for (int i = (n - 1 - 1) / 2; i >=0; i--){AdjustDown(hp->a, n, i);}
}
有创建肯定要有销毁,不然会内存泄漏
// 堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);free(hp->a);hp->a = NULL;hp->capacity = hp->size = 0;
}判断是不是空堆
// 堆的判空
int HeapEmpty(Heap* hp)
{assert(hp);return hp->size == 0;
}堆的插入(尾插)
把一个接点放进去还要考虑这个节点可能会比他的父节点还大,所以他就要开始篡改族谱了...
和爸爸,爷爷...都比较一下,谁更大谁就在在上面,所以要一个函数:向上调整(还是以大堆为例)
//向上调整,大堆
void AdjustUp(HPDataType* a, int child)
{assert(a);int parent = (child - 1) / 2;while (child>=0){if (a[child] > a[parent]){Swap(&a[child],& a[parent]);child = parent;parent= (child - 1) / 2;}else{break;}}
}所以堆插就是
// 堆的插入,尾插
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->capacity == hp->size){//需要扩容int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;HPDataType* newnode = (HPDataType*)realloc(hp->a,sizeof(HPDataType) * newcapacity);if (newnode == NULL){perror("malloc fail");exit(-1);}hp->a = newnode;hp->capacity = newcapacity;}hp->a[hp->size] = x;hp->size++;//向上调整AdjustUp(hp->a, hp->size - 1);
}堆的删除
不能简单覆盖,这样你千辛万苦的父子关系全乱套了
所以先把最后一个节点和根换一下,然后尾删直接把size--
之后就该考虑一下向下调整的问题
// 堆的删除
void HeapPop(Heap* hp)
{assert(hp);assert(!HeapEmpty(hp));Swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;AdjustDown(hp->a, hp->size, 0);
}取堆顶的数据
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);return hp->a[0];
}堆数据个数
// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->size;
}找出前k个最大
//找出前k个最大
void PrintTopK(int* a, int n, int k)
{assert(a);Heap hp;while (k--){HeapCreate(&hp, a, k);}
}最后最后完整的实现在下面
include "Heap.h"//打印
void HeapPrint(Heap* hp)
{assert(hp);for (int i=0;isize;i++){printf("%d ", hp->a[i]);}printf("\n");
}
//交换
void Swap(HPDataType* a, HPDataType* b)
{HPDataType tmp = *a;*a = *b;*b = tmp;
}// 堆的判空
int HeapEmpty(Heap* hp)
{assert(hp);return hp->size == 0;
}// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{assert(hp);hp->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (hp->a == NULL){perror("HeapCreate fail");exit(-1);}memcpy(hp->a, a, n*sizeof(HPDataType));hp->size = hp->capacity=n;for (int i = (n - 1 - 1) / 2; i >=0; i--){AdjustDown(hp->a, n, i);}
}
//初始化
void HeapInit(Heap* hp)
{assert(hp);hp->a = NULL;hp->capacity = hp->size = 0;
}// 堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);free(hp->a);hp->a = NULL;hp->capacity = hp->size = 0;
}//向上调整,大堆
void AdjustUp(HPDataType* a, int child)
{assert(a);int parent = (child - 1) / 2;while (child>=0){if (a[child] > a[parent]){Swap(&a[child],& a[parent]);child = parent;parent= (child - 1) / 2;}else{break;}}
}
// 堆的插入,尾插
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->capacity == hp->size){//需要扩容int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;HPDataType* newnode = (HPDataType*)realloc(hp->a,sizeof(HPDataType) * newcapacity);if (newnode == NULL){perror("malloc fail");exit(-1);}hp->a = newnode;hp->capacity = newcapacity;}hp->a[hp->size] = x;hp->size++;//向上调整AdjustUp(hp->a, hp->size - 1);
}//向下调整
AdjustDown(HPDataType* a, int n, int parent)
{assert(a);int child = 2 * parent + 1;//假设是左孩子,并且左孩子是最大的孩子while (child a[child] && child+1a[0], &hp->a[hp->size - 1]);hp->size--;AdjustDown(hp->a, hp->size, 0);
}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);return hp->a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->size;
}
//找出前k个最大
void PrintTopK(int* a, int n, int k)
{assert(a);Heap hp;while (k--){HeapCreate(&hp, a, k);}
}
学会了吗??不懂的留言~
