目录

思考题4）原题目：贝叶斯判别的基本思想是什么？

练习题第3题:以舒张期血压和讯将胆固醇含量预测被检查者是否患冠心病，测得15名冠心病人和16名健康人的舒张压。X1及血浆胆固醇含量X2，结果如表6-4。

练习题第4题:对于A股市场2009年陷入财务困境的上市公司（ST公司），我们收集了8间ST公司陷入财务困境前的一年（2008年）的财务数据，同时对于财务良好的公司（非ST公司），收集了同一时期8家非ST公司对应的财务数据。如表6-5所示：

思考题4）原题目：贝叶斯判别的基本思想是什么？

答：贝叶斯判别是根据最小风险代价判决或最大似然比判决，是根据贝叶斯准则进行判别分析的一种多元统计分析法。因为贝叶斯思想具有一定的“主观性”，使得贝叶斯统计变的强大且便利，其优势在于：即使在数据很少的情况下也可以进行推测，随着数据量的增大推测也会越来越准确并对所做信息做出瞬时反应，自动升级推测。

其基本思想是：

设有两个总体，它们的先验概率分别为、，各总体的密度函数为、在观测到一个样本x的情况下，可用贝叶斯公式计算它来自第k个总体的后验概率为：

一种常用判别准则是：对于待判样本x，如果在所有的中 是最大的，则判定属于第总体。通常会以样本的频率作为各总体的先验概率。

练习题第3题:以舒张期血压和讯将胆固醇含量预测被检查者是否患冠心病，测得15名冠心病人和16名健康人的舒张压。X1及血浆胆固醇含量X2，结果如表6-4。

答：

前期准备：首先读入数据：

> library(readxl)

> E6.03<- read_excel("D:/Desktop/6.4.xlsx",  sheet = "E6.03")

> View(X6_4)

> attach(E6.03) 

（1） 对每一组数据用不同的符号作两变量的散点图，观察它们在平面上的散布情况，并判断对该组数据做判别分析是否合适？

 >plot(x1,x2)  #绘散点图

 > text(x1,x2,Y,adj = -0.5)     #标记处途中原始点

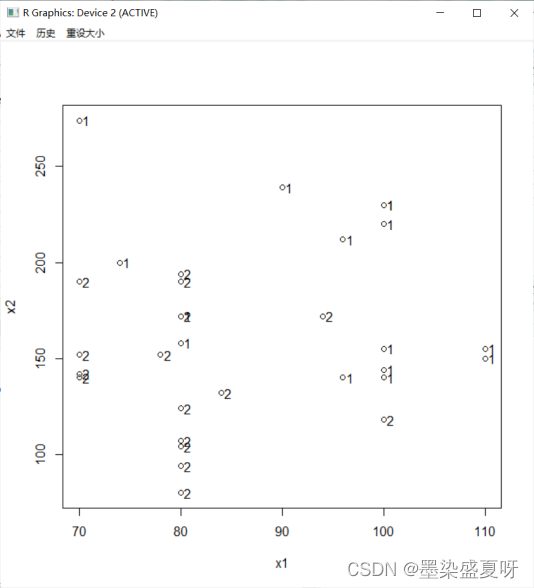
1与2分割较为明显，适合做判别分析。

（2） 分别建立距离判别（等方差阵和不等方差阵）、Fisher判别和Bayes判别分析模型，计算各自的判别符合率，以此确定哪种判别方法最恰当。

  假设两类总体都服从正态分布。

<1>距离判别，与Fisher判别、先验概率为频率的Bayes判别等价。

 > library(MASS)   #距离判别模型,注意，若想要运行下面命令，要先导包才可

 > ld=lda(y~x1+x2, data=E6.03);ld

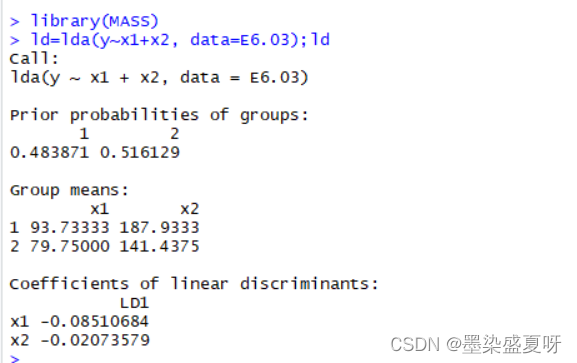
> lp = predict(ld) # 在原训练集上 预测

> G1 = lp$class      # 判别结果

> tab1 = table(y, G1)# 判别矩阵

> tab1

>sum(diag(prop.table(tab1))) # 判对率

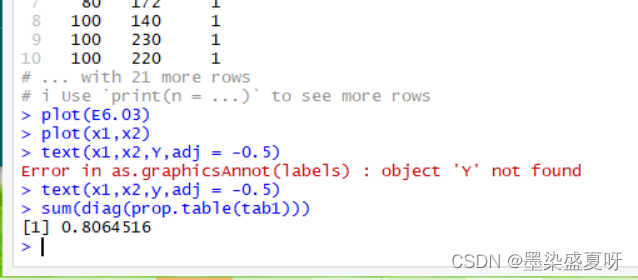
<2>Fisher判别分析

> lda_1 = lda(y ~ x1 + x2)

> lda_1

> pre2 = predict(lda_1)

> Y6 = pre2$class

> tab2 = table(y,Y6)

> tab2    # 判别矩阵

>sum(diag(tab2))/sum(tab2) # 判对率

<3>先验概率相同的Bayes判别

> lda_2 = lda(y ~ x1 + x2,prior = c(1,2)/3)

> lda_2  

> pre3 = predict(lda_2)

> Y7 = pre3$class

> tab3 = table(y,Y7)

> tab3

>sum(diag(tab2))/sum(tab3) # 判对率

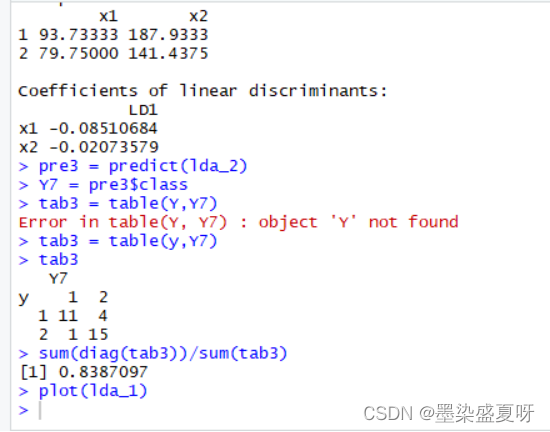
综上所述，由以上结果，根据各自的判别符合率大小可知，距离判别最恰当。

（3）绘制线性判别函数图

> plot(lda_1)

练习题第4题:对于A股市场2009年陷入财务困境的上市公司（ST公司），我们收集了8间ST公司陷入财务困境前的一年（2008年）的财务数据，同时对于财务良好的公司（非ST公司），收集了同一时期8家非ST公司对应的财务数据。如表6-5所示：

数据涉及四个变量：资产负债率x1 、流动资产周转率x2 、总资产报酬率x3 和营业收入增长率x4。类别变量G中2代表ST公司，1代表非ST公司。

导入数据：

数据查看：

> dim(l6_5)#用于获取l6_5数据的维度

> duplicated(l6_5)#用于去重，标记TRUE的位置则表明数据重复

> l4<-unique(l6_5) #去除相同的行

1. 分别建立线性判别，非线性判别和Bayes判别分析模型，计算各自的判别符合率，确定哪种方法最适合；

线性判别：

> library(MASS)  #导入MASS包

> ld=lda(G~x1+x2+x3+x4,data = l6_5) # 建立线性判别模型

> lp=predict(ld) # 根据线性判别模型预测所属类别

> G1=lp$class  # 预测的所属类别结果

> t1=table(G,G1) # 生成判别矩阵

> t1 # 查看判别矩阵

> r1=sum(diag(t1)/sum(t1)) # 计算判对率

> r1  # 查看判对率

非线性判别：

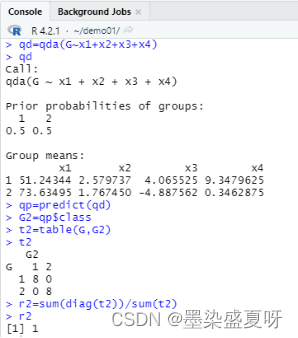
> qd=qda(G~x1+x2+x3+x4) # 建立非线性判别模型(二次判别)

> qd

> qp=predict(qd) # 根据非线性判别模型预测所属类别

> G2=qp$class # 预测的所属类别结果

> t2=table(G,G2) # 生成判别矩阵

> t2

> r2=sum(diag(t2))/sum(t2) # 计算判对率

> r2

Bayes判别：

假设两类总体均服从正态分布。则先验概率为频率的Bayes与线性判别的判别结果相同，下面建立先验概率相同的Bayes判别分析模型。

> ld2=lda(G~x1+x2+x3+x4,prior=c(1,1)/2,data = l6_5)# 建立 Bayes判别模型 (先验概率相等的情况)

> lp2=predict(ld2) # 根据Bayes判别模型预测所属类别

> ld2

> G3=lp2$class  # 预测的所属类别结果

> t3=table(G,G3) # 生成判别矩阵

> t3

> r3=sum(diag(t3))/sum(t3);r3  # 计算判对率

总结：由上述建立线性判别，非线性判别和Bayes判别分析模型，计算各自的判别符合率r1=0.875,r2=1,r3=0.875可知非线性判别分析模型最恰当。

1. 某公司2008年财务数据为：x1:78.3563,x2:0.8895,x3:1.8001,x4:14.1022。试判定2009年该公司是否会陷入财务困境。

> predict(ld,data.frame(x1=78.3563,x2=0.8895,x3=1.8001,x4=14.1022))

总结：由上述预测结果判定为2可知->(陷入危机)的概率为87%，可信，2009年该公司会陷入财务困境。

> detach(l6_5) # 使用完毕，解绑

结束！